Le tunning des hyperparamètres

De la grille de recherche à l'optimisation bayésienne, trouvez les paramètres d'ajustement adéquats pour optimiser l'apprentissage de vos modèles

Que ce soit un algorithme XGBoost, un random forest ou encore un réseau de neurones, vous disposez d'un certain nombre de paramètres d'entrée qui vont constituer autant d'ajustements possibles. Chercher à optimiser la valeur de ces paramètres relève bien souvent d'une démarche empirique dont l'efficacité peut laisser perplexe. Il existe cependant quelques méthodes plus ou moins efficaces pour tenter d'ajuster ces hyperparamètres. Désigné en anglais sous le terme de tunning, nous allons voir en quoi consiste cette démarche.

Données de travail

Nous allons travailler avec un dataset regroupant 5891 transactions immobilières de la ville de Daegu en Corée du Sud. Ces données sont publiques et proviennent d'une source gouvernementale accessible sur le site data.go.kr Pour chaque bien nous disposons, en plus du prix de vente, d'un certain nombre d'informations comme par exemple l'année de vente, l'année de construction, l'étage du bien, la surface, le nombre de parking, etc ...
En voici un extrait :

Chargeons tout d'abord les librairies dont nous aurons besoin pour cette première partie :

import pandas as pd
import numpy as np
from sklearn.model_selection import validation_curve
from sklearn.ensemble import RandomForestRegressor
import matplotlib.pyplot as plt

Chargeons ensuite nos données puis éditons en un extrait :

data = pd.read_csv('Daegu_Real_Estate_data.csv', sep=',')
data.head()

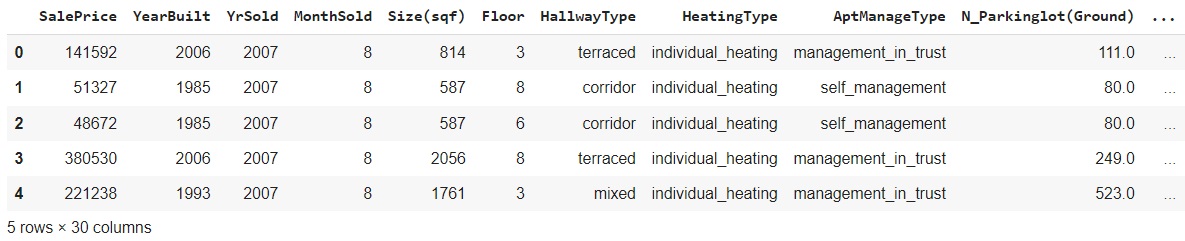
Au total, nous avons donc 5891 observations et 30 colonnes dont le prix du bien. Nous allons, dans le cadre de cet exemple, mettre de côté les colonnes non numériques. Nous pourrions bien entendu les encoder, comme nous l'avions d'ailleurs expliqué dans un précèdent article "Variables catégorielles et régression". Cependant les variables quantitatives nous suffiront pour cerner le sujet de cet article.

#Le prix du bien est notre variable reponse
y = data.SalePrice

#Nous ne conservons comme predicteurs que les variables numeriques
X = data._get_numeric_data()
X = X.drop(['SalePrice'], axis=1)

Notre modèle : un random forest

Nous allons travailler avec un régresseur random forest dont l'objectif sera de prédire le prix d'un bien en fonction de ses caractéristiques. Pour cela nous allons bien sur l'entrainer sur une partie du dataset. Cependant il nous faut au préalable initialiser un certain nombre de paramètres d'entrée propres au random forest. Voyons tout d'abord quels sont les paramètres que nous allons tâcher d'optimiser. Pour chacun d'entre eux, nous éditerons l'évolution de l'erreur absolue moyenne (MAE) pour le set de validation ainsi que le set d'apprentissage, en faisant évoluer le paramètre testé.

Pour nous faciliter la tâche, nous allons créer deux fonctions. Une première qui va instancier un modèle et l'entrainer sous le contrôle de la méthode validation_curve. Il suffira de passer à cette dernière le paramètre a tester et le range de valeurs désirées. Par défaut une cross-validation de 5 folds sera implémenté. La seconde fonction nous permettra de dresser les courbes associées :

Notre fonction d'instanciation et d'exécution du modèle :

def runForest(param_name, param_range):
  #Instanciation du modele
  rf = RandomForestRegressor()

  #Calcul des scores
  forest_train_scores, forest_validation_scores = validation_curve(rf, X, y,
                                              param_name=param_name,
                                              param_range=param_range,
                                              scoring="neg_mean_absolute_error",
                                              n_jobs=2)

  return {'train': -forest_train_scores, 
          'val': -forest_validation_scores}

A présent, notre fonction de traçage des courbes de suivi :

def plotCurves(forestErrors, param_name) :
  fig, ax = plt.subplots(1, figsize=(7,7))
  plt.errorbar(param_range, forestErrors['train'].mean(axis=1), label="Apprentissage")
  plt.errorbar(param_range, forestErrors['val'].mean(axis=1), label="Validation")
  plt.title("Random forest MAE / "+param_name)
  plt.legend()
  _ = fig.suptitle("Validation curves", y=1.1)

Ceci étant fait, passons en revue les hyperparamètres sur lesquels nous allons travailler.

La profondeur maximale (MAX_DEPTH)

Comme son nom l'indique, il s'agit de la profondeur maximale à laquelle notre arbre va pouvoir se développer. Par profondeur maximale, il faut comprendre le chemin le plus long entre la racine et une feuille.
Nous allons faire varier cette dernière de 1 à 50 et calculer l'erreur moyenne.

param_name = "max_depth"
param_range = np.arange(1, 50)

forestErrors = runForest(param_name, param_range)
plotCurves(forestErrors, param_name)

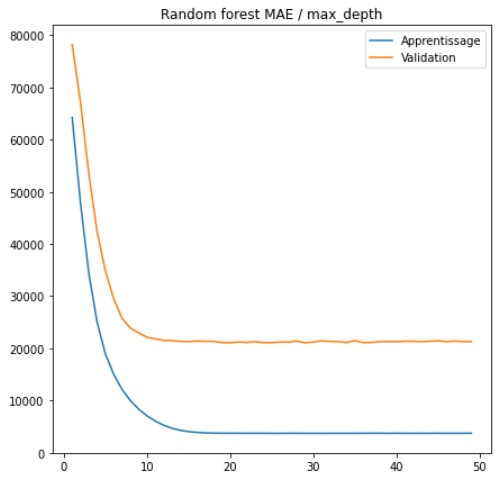
L'erreur absolue moyenne diminue très rapidement avec l'augmentation de la profondeur de l'arbre, cependant elle finit par stagner à partir d'une profondeur de 10. On peut en conclure que l'augmentation de la profondeur maximale n'aide pas, au-delà d'une certaine valeur, le modèle à généraliser pour performer sur le set de test. C'est d'ailleurs tout le problème qui nous occupe car, en effet, une croissance excessive de l'arbre de décision aura pour conséquence un surajustement aux données d'apprentissage. Il nous faut limiter cette croissance tout en laissant à l'algorithme suffisamment d'espace pour généraliser.

Nombre minimum d'observations pour scission (MIN_SAMPLES_SPLIT)

A chaque noeud, l'arbre aura la possibilité de se développer, sous réserve que le paramètre MAX-DEPTH, vu précédemment le lui permet. Le paramètre MIN_SAMPLES_SPLIT va indiquer à l'arbre le nombre minimal d'observations courantes en-dessous duquel il ne pourra plus scinder l'échantillon pour créer de nouveaux nœuds.
Comme précédemment, procédons au même test en faisant évoluer le paramètre min_samples_split. Précisons que ce paramètre, s'il est entier constitue un nombre d'observations et s'il est décimal, un pourcentage de l'effectif.

param_name = "min_samples_split"
param_range = np.linspace(0.1, 1.0, 10, endpoint=True)

forestErrors = runForest(param_name, param_range)
plotCurves(forestErrors, param_name)

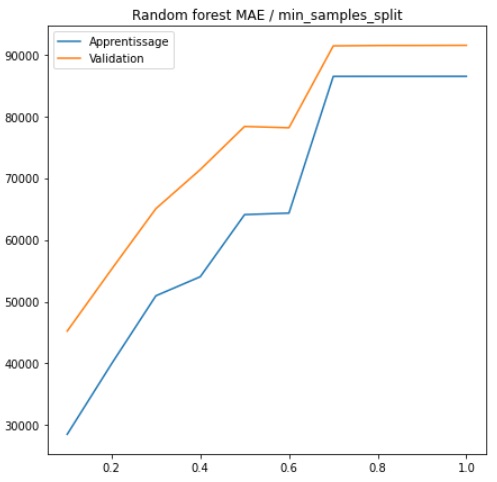
L'erreur absolue moyenne augmente continuellement pour attendre un palier à 70% des effectifs. Nous sommes alors en situation de sous-apprentissage.

Nombre de caracteristiques (MAX_FEATURES)

Il s'agit tout simplement du maximum de caractéristiques que l'algorithme peut tester dans un arbre. Nous avons 23 caractéristiques numériques, nous allons donc apprécier l'évolution de l'erreur moyenne en faisant varier ce paramètre de 1 à 23 :

param_name = "max_features"
param_range = np.arange(1,23)

forestErrors = runForest(param_name, param_range)
plotCurves(forestErrors, param_name)

Dans notre cas, nous constatons sur le set de validation une diminution d'erreur moyenne jusqu'à 17 variables explicatives. Au-delà, la mae commence à repartir à la hausse.

Nombre d'arbres (N_ESTIMATORS)

Enfin nous allons tenter d'ajuster le nombre d'arbres que l'algorithme sera en mesure de générer. Un nombre d'arbres élevé, bien que supposément plus efficace, peut augmenter drastiquement le temps d'exécution. Il s'agit alors de trouver le bon arbitrage entre performance et complexité.

param_name = "n_estimators"
param_range = np.arange(1, 50, 5)

forestErrors = runForest(param_name, param_range)
plotCurves(forestErrors, param_name)

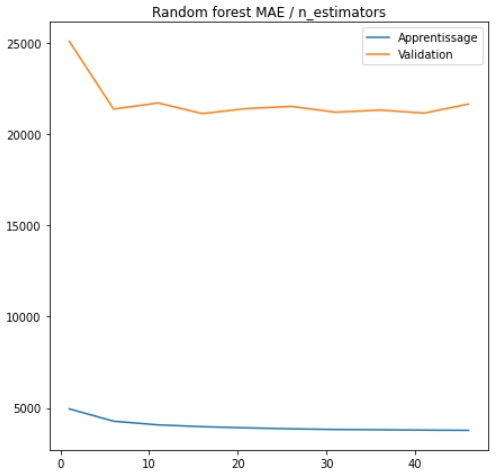
L'erreur moyenne diminue rapidement jusqu'à 6 arbres puis on observe une stagnation.

Grilles de paramètres

Nous venons de passer en revue quatre paramètres que propose le random forest. Il y en d'autres mais nous nous contenterons de ceux-là dans le cadre de cet article. En testant chacun de ces paramètres individuellement nous avons une vague idée d'une fourchette optimum potentielle, néanmoins cela se complique lorsqu'il s'agit d'évaluer des combinaisons.
Il existe pour cela la notion de grille, qui consiste en un dictionnaire dont les clés sont les noms des paramètres à tester et les valeurs, des vecteurs des valeurs de chacun des paramètres. Nous allons étudier trois stratégies possibles de tunning utilisant ces grilles.

Grid Search : Toutes les combinaisons sur un nombre restreints de valeurs

La première stratégie consiste à indiquer pour chaque paramètre un nombre restreint de valeurs puis d'exécuter un gridsearch qui va tout simplement tester toutes les combinaisons possibles.

Auparavant, et puisque nous ne l'avons pas encore fait, séparons nos données en deux sets destinés à l'apprentissage et à la validation, selon un rapport respectif de 80/20 :

from sklearn.model_selection import train_test_split
X_train, X_valid, y_train, y_valid = train_test_split(X, y, train_size=0.8, test_size=0.2)

A présent, implémentons notre gridsearch :

from sklearn.model_selection import GridSearchCV

# Initialisation des parametres a tester
param_grid = {
    'max_depth': [5, 15, 30, 60, 80, 100],
    'max_features': [3, 10, 15, 20],
    'min_samples_split': [30, 100, 300, 600],
    'n_estimators': [2, 4, 12, 24, 48, 80, 100]
}

# Instanciation du random forest
rf = RandomForestRegressor()

# Instantiation du modele grid search 
grid_search = GridSearchCV(estimator = rf, param_grid = param_grid, 
                          cv = 3, n_jobs = -1, verbose = 2)

# Execution du gridsearch sur les donnees
grid_search.fit(X_train, y_train)

Dans le code ci-dessus, vous constatez que nous avons stipulé 4 à 6 valeurs par paramètre et non une fourchette comme nous l'avions fait lors de la revue précédemment. Notre grille param_grid, telle qu'elle est définie, représente déjà 672 combinaisons.
Nous instancions ensuite un modèle random forest que le gridsearch utilisera comme estimateur. Le gridsearch prend en entrée notre grille mais également le nombre de fold, c'est à dire le nombre de réagencements apprentissage/validation qu'il va effectuer au sein des données. Il s'agit de la cross-validation.

Le message qui apparait à l'exécution :

Fitting 3 folds for each of 672 candidates, totalling 2016 fits

L'ajustement aux données étant terminé, voyons quels sont les meilleurs paramètres que le gridsearch a trouvé :

grid_search.best_params_

{'max_depth': 15,
 'max_features': 20,
 'min_samples_split': 30,
 'n_estimators': 80}

Le résultat parle de lui-même. Il s'agit de la meilleure des 672 combinaisons, affichons son erreur absolue moyenne :

from sklearn import metrics

best_grid = grid_search.best_estimator_

best_rf = best_grid.fit(X_train, y_train)
y_preds = best_rf.predict(X_valid)

print('Mean Absolute Error:', metrics.mean_absolute_error(y_valid, y_preds))  

Mean Absolute Error: 11297.499263034239

Nous obtenons une erreur moyenne de près de 11000 dollars pour un bien, ce qui constitue une très bonne performance. Avouons toutefois que nous avions au préalable effectué un travail d'analyse en testant nos paramètres.

Random Search : Des combinaisons au hasard sur un nombre élevés de valeurs

Notre première stratégie consistait à tester toutes les combinaisons sur la base de valeurs entrées, nous obligeant, par conséquent, à limiter ces dernières. Cette fois, nous allons spécifier des fourchettes de valeurs. Aussi, le modèle de grille ne va pas tester toutes les combinaisons possibles mais des combinaisons prises au hasard :

from sklearn.model_selection import RandomizedSearchCV

# Initialisation des parametres a tester
param_grid = {
    'max_depth': np.arange(1, 100),
    'max_features': np.arange(1,23),
    'min_samples_split': np.arange(1,3000),
    'n_estimators': np.arange(1, 100, 5)
}

# Instanciation du random forest
rf = RandomForestRegressor()

# Instantiation du modele random search 
grid_random = RandomizedSearchCV(estimator = rf, param_distributions = param_grid, 
                                 cv = 3,  n_jobs = -1, verbose=2)
# Execution du random search sur les donnees
grid_random.fit(X_train, y_train)

Dans le code ci-dessus, vous constatez que nous reprenons la même logique que précédemment à la différence que notre grille est initialisée sur la base de fourchettes de valeurs.
Nous instancions ensuite un modèle RandomizedSearchCV. Le reste est identique. Voyons les meilleurs paramètres trouvés :

grid_random.best_params_

{'n_estimators': 21,
 'min_samples_split': 415,
 'max_features': 14,
 'max_depth': 86}

Nous constatons que nos paramètres sont différents du gridsearch. Voyons l'erreur absolue moyenne qui en résulte :

best_grid = grid_random.best_estimator_
best_rf = best_grid.fit(X_train, y_train)
y_preds = best_rf.predict(X_valid)
print('Mean Absolute Error:', metrics.mean_absolute_error(y_valid, y_preds)) 

Mean Absolute Error: 26015.94391589906

Le gridsearch fait pour l'instant mieux. Passons à notre dernière stratégie.

Optimisation bayésienne

L'inférence bayésienne repose sur la prise en compte des résultats passés pour explorer un domaine de solutions possibles. Cette optimisation va tenter, en quelques sortes, de maximiser incrémentalement une fonction objectif sur la base d'un scoring qu'on lui aura au préalable donné. Dans notre cas la fonction objectif va se reposer sur le résultat d'une cross validation d'un régresseur random forest.

Installons tout d'abord le package contenant BayesianOptimization :

pip install bayesian-optimization

Nous importons ensuite les librairies nécessaires :

from bayes_opt import BayesianOptimization
from sklearn.model_selection import cross_val_score

Enfin nous implémentons l'optimisation :

def fObjectif(X, y, **kwargs):
    estimator = RandomForestRegressor(**kwargs)
    cval = cross_val_score(estimator, X, y, scoring = 'neg_mean_absolute_error', cv = 4, verbose = 2, n_jobs = -1)
    return cval.mean()

def bayesian_rf(X, y, n_iter = 100):
    def rf_crossval(max_depth, min_samples_split, max_features, n_estimators):

        return fObjectif(
            X = X,
            y = y,
            max_depth = int(max_depth),
            min_samples_split = int(min_samples_split),
            n_estimators = int(n_estimators),
            max_features = int(max_features)
        )
    
    optimizer = BayesianOptimization(
        f = rf_crossval,
        pbounds = {
            "max_depth" : (1, 100),
            "min_samples_split" : (1, 3000),
            "max_features" : (1, 23),            
            "n_estimators" : (1, 100)
        }
    )
    return optimizer

Comme vous le constatez, nous avons implémenté deux fonctions. Tout d'abord la fonction objectif, dans laquelle nous instancions un modèle random forest puis, via une cross validation à 4 fold, calculons les erreurs absolues moyennes. Le résultat sera la moyenne des MAE obtenues.

Nous avons ensuite implémenté l'appel à la fonction BayesianOptimization via ce que l'on appelle un wrapper, c'est à dire une encapsulation de fonction. Les paramètres que nous passons ont pour valeurs les mêmes fourchettes que celles qui nous ont servies pour le random grid. Lançons à présent l'exécution du modèle, sur une base de 300 itérations :

optimizer = bayesian_rf(X_train, y_train, n_iter = 300)
optimizer.maximize(n_iter = 300)

L'exécution prend plus de temps que les grid search et random search. Voyons les meilleurs paramètres trouvés :

bayesian_params = optimizer.max['params']
bayesian_params

{'max_depth': 30.507324428124065,
 'max_features': 18.05601609255998,
 'min_samples_split': 3.09682499720257,
 'n_estimators': 71.41071821881003}

Enfin, calculons l'erreur absolue moyenne obtenue sur le set de validation :

rf = RandomForestRegressor(max_depth = int(round(bayesian_params["max_depth"], 0)),
                           min_samples_split = int(round(bayesian_params["min_samples_split"], 0)),
                           max_features = int(round(bayesian_params["max_features"], 0)), 
                           n_estimators=int(round(bayesian_params["n_estimators"], 0)),
                           n_jobs=-1)

rf.fit(X_train, y_train)
y_preds = rf.predict(X_valid)
from sklearn import metrics
print('Mean Absolute Error:', metrics.mean_absolute_error(y_valid, y_preds))

Mean Absolute Error: 9664.041309336408

Nous avons réussi à faire mieux que le gridsearch bien que, cette fois, nous ne nous sommes pas souciés des paramètres d'entrée.

Retrouvez dans la rubrique "Nos datasets" toutes les données dont vous aurez besoin pour tester et pratiquer !