Variables catégorielles et régression
Comment gérer vos variables catégorielles dans vos modèles de régression sous Python ?
Lorsqu'il s'agit d'entrainer un modèle de régression, une des premières questions qui s'impose
concerne la gestion des variables catégorielles. Comme vous le savez, en effet, elles ne peuvent être
inclues dans la liste des variables explicatives en l'état. Aussi, plusieurs solutions s'offrent à vous.
Nous allons dans cet article donner 3 pistes à exploiter. Pour ce faire nous allons pour chacune d'entre elles,
les soumettre à un modèle de type random forest et constater la performance prédictive obtenue sur la base
de l'erreur absolue moyenne.
Données de travail
Nous allons travailler avec le dataset d'une liste de 150 transactions immobilières. Pour chaque appartement,
nous disposons du nombre de chambres, de salles de bain et de places de stationnement, nous disposons
également de la surface, de l'étage ainsi que du nombre d'étages total de l'immeuble. Enfin nous disposons
de 2 variables catégorielles, la présence d'un balcon (2 modalités : oui ou non) et le type de chauffage
(3 modalités : gaz, électrique ou pompe à chaleur). La variable à prédire est le prix de vente de l'appartement.
Ce dataset est disponible sur gorenja.com ici.
Voici un extrait du dataset :
import pandas as pd
data = pd.read_csv('appartements.csv', sep=';')
data.head()
bien chb sdb surface parking balcon chauffage etage etage_imm prix 0 REF23978 2 1 30 1 non gaz 1 5 99000 1 REF35989 2 1 30 2 non electrique 4 7 158000 2 REF34600 2 1 53 1 non gaz 10 12 348000 3 REF24544 1 1 33 1 oui gaz 9 11 120000 4 REF30844 3 1 44 1 oui gaz 10 11 195000
Préparation des données
En termes de préparation, nous allons tout d'abord séparer une première fois nos données pour isoler
la variable d'intérêt, le prix. Nous allons ensuite les séparer une seconde fois pour constituer un set
d'entrainement et un set de test, sur la base d'une proportion 80/20.
from sklearn.model_selection import train_test_split
#nous isolons le prix, et supprimons l'identifiant du bien
y = data.prix
X = data.drop(['bien', 'prix'], axis=1)
#nous constituons un set d'entrainement et un set de test
X_train, X_valid, y_train, y_valid = train_test_split(X, y, train_size=0.8, test_size=0.2)
Modèle et évaluation
Nos données sont prêtes. Il ne nous reste plus qu'à définir une fonction dans laquelle nous allons instancier un modèle de régression random forest, l'entrainer sur les données que nous les passerons en paramètres et enfin évaluer les prédictions qu'il fera sur le set de test en les comparant aux valeurs réelles.
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
def regression(X_train, X_valid, y_train, y_valid):
model = RandomForestRegressor(n_estimators=100)
model.fit(X_train, y_train)
preds = model.predict(X_valid)
return mean_absolute_error(y_valid, preds)
Voyons à présent ce que nous pouvons faire de nos 2 variables balcon et chauffage, inexploitables en l'état.
Solution 1 : Les supprimer
C'est la solution la plus simple en effet. Cela peut paraitre un peu radical, surtout si l'on considère que
la ou les variables en question peuvent être porteuses d'informations et donc discriminantes. Cependant cette
solution mérite d'être étudiée dans au moins 2 cas de figure.
La suppression d'une variable catégorielle peut, en effet, être envisagée si celle-ci présente un certain nombre
de valeurs manquantes. Leur imputation étant impossible, l'utilisation de cette variable sera en effet peu pertinente,
voir contre-productive.
Le second point sur lequel il faut faire attention est le déséquilibre éventuel des modalités d'une variable catégorielle. En
effet, si une des modalités venait a être sous-représentée, il se peut très bien qu'aucune observation ne soit présente dans le
set d'entrainement, ou du moins pas suffisamment pour que le modèle soit pertinent. Outre la suppression pure et simple de la
variable, une autre solution serait alors de pratiquer une cross-validation en K-fold par exemple.
Ceci étant dit, procédons à la suppression de nos 2 variables balcon et chauffage et exécutons notre modèle :
#Suppression des variables categorielles des 2 sets (entrainement et test)
X_trainV1 = X_train.drop(['balcon', 'chauffage'], axis=1)
X_validV1 = X_valid.drop(['balcon', 'chauffage'], axis=1)
#Execution du modele
print("Version 1 : supression des variables categorielles")
print(regression(X_trainV1, X_validV1, y_train, y_valid))
Version 1 : supression des variables categorielles 46647.666666666664
Solution 2 : Codage ordinal
Comme vous le savez, une variable ordinale est une variable qualitative numérique. Le principe ici est donc, tout simplement, d'associer à chaque modalité de la variable catégorielle une valeur numérique.
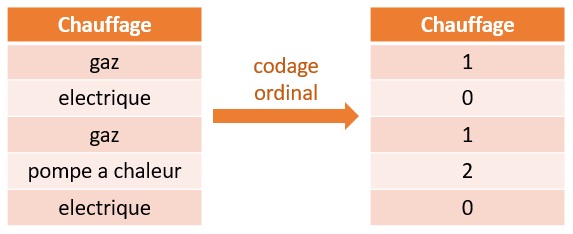
L'opération peut aisément être réalisée via la fonction dédiée de scikit learn :
from sklearn.preprocessing import OrdinalEncoder
#Instanciation du transformeur
ordinal_encoder = OrdinalEncoder()
#Duplication des sets originaux
X_trainV2 = X_train.copy()
X_validV2 = X_valid.copy()
#Codage ordinal des 2 variables categorielles
X_trainV2[['balcon', 'chauffage']] = ordinal_encoder.fit_transform(X_trainV2[['balcon', 'chauffage']])
X_validV2[['balcon', 'chauffage']] = ordinal_encoder.transform(X_validV2[['balcon', 'chauffage']])
#Execution du modele
print("Version 2 : encodage ordinal")
print(regression(X_trainV2, X_validV2, y_train, y_valid))
Version 2 : encodage ordinal 44396.0
Solution 3 : Codage disjonctif complet
L'encodage disjonctif complet (ou One Hot Encoding) va consister, pour une variable catégorielle, à créer autant de colonnes que de modalités. Chaque colonne prendra ensuite une valeur booléenne selon la modalité courante. Voici un exemple concret :
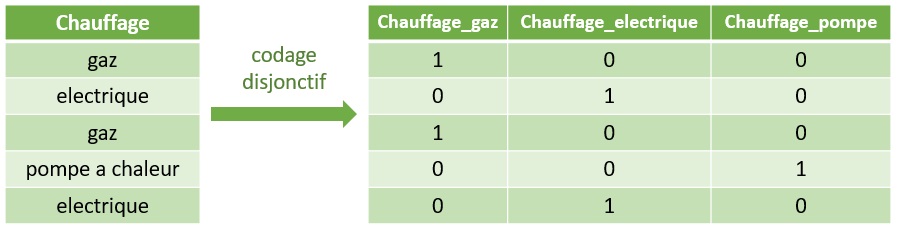
A la différence du codage ordinal, la colonne originale disparait, ou du moins, il est nécessaire de la supprimer. Par ailleurs,
le modèle a accès a l'information contraire, sous-entendue dans le codage ordinal. Sur la première ligne de l'exemple
ci-dessus, il ressort en effet que l'appartement ne dispose pas du chauffage électrique, c'est clairement stipulé.
A l'instar du codage ordinal, le codage disjonctif peut également être réalisé simplement via Pandas cette fois-ci. Notez
par ailleurs que Pandas se charge de la suppression de la colonne encodée :
# Encodage disjonctif
X_trainV3 = pd.get_dummies(data=X_train, columns=['balcon', 'chauffage'])
X_validV3 = pd.get_dummies(data=X_valid, columns=['balcon', 'chauffage'])
print("Version 3 : encodage disjonctif complet")
print(regression(X_trainV3, X_validV3, y_train, y_valid))
Version 3 : encodage disjonctif complet 44111.666666666664
Conclusion
Dans le test que nous avons mené, l'encodage disjonctif présente le meilleur résultat, suivi de l'encodage ordinal puis de la suppression. Ce classement est régulièrement respecté, cependant tout dépend bien entendu du set de données, de sa taille, de la représentation des modalités, etc ... Il conviendra de bien appréhender les données avant toute chose.
Retrouvez dans la rubrique "Nos datasets" toutes les données dont vous aurez besoin pour tester et pratiquer !

