ACP sous R
Une étude de cas pour réaliser une analyse en composantes principales (ACP) sous R
L'analyse en composantes principales, dite plus simplement ACP, est une méthode factorielle
d'analyse descriptive multivariée. Son objectif premier est de réduire le nombre de variables
d'analyse tout en conservant au maximum l'information. Pour y parvenir, l'ACP va créer des nouvelles
dimensions en réunissant les variables corrélées entre elles.
L'objet de cet article n'est pas d'étudier la théorie sous-jacente à l'ACP mais de dérouler un
cas pratique sous R.
Environnement de travail
Nous allons réaliser notre ACP en utilisant le plugin Factominer depuis R Commander. Pour ce faire nous nous rendons sur notre console R puis installons, si ce n'est déjà fait, la librairie R Commander (Rcmdr) puis Factominer (RcmdrPlugin.FactoMineR) :
install.packages(c(« Rcmdr », « RcmdrPlugin.FactoMineR »))
Ceci étant fait, nous lançons R Commander à présent :
library(« Rcmdr »)
Depuis l'interface de R Commander, nous nous rendons dans le menu Outils puis Chargement des plugins. Nous
sélectionnons FactoMineR. Un message nous indique que R Commander doit redémarrer, nous acceptons.
Lorsque R commander a redémarré, un nouveau menu « FactoMineR » est apparu.
Nous n’allons pas rencontrer de difficulté avec le dataset dont il va être question dans cet article, cependant, il se peut que, pour certains jeux de données volumineux, un manque de mémoire vive peut survenir. Il convient alors d’étendre la mémoire maximum allouée à R avec les commandes ci-dessous :
Vérification de la mémoire limite paramétrée :
memory.limit(size = NA)
Allocation de plus de mémoire :
memory.limit(size = 11000)
Encore une fois, vous n'aurez normalement pas besoin de ces dernières lignes de code. Néanmoins cela pourra vous être utile un jour peut-être.
Données de travail
Nous allons travailler avec un jeu de données présentant un certain nombre d'indicateurs portés sur le secteur agricole de 28 pays d'Europe, dont le Royaume-Uni. Ces données couvrent l'année 2016 et sont fournies par Eurostat. Le dataset est disponible ici. Vous trouverez par ailleurs dans la section crédits de cet article le lien vers la licence à laquelle l'exploitation de ces données est soumise.
Le dataset compte 28 pays et 24 colonnes dont voici les détails:
| Country | Nom du pays |
| farms_number | Nombre d'exploitations agricoles |
| used_agricultural_area_ha | Surface exploitée (en hectares) |
| standard_output_EUR | Production standard, c'est à dire la valeur monétaire moyenne de la production agricole (en euros) |
| subsistence_semisubsistence_farms | Nombre d'exploitations agricoles qui consomment plus de 50% de la production |
| total_labour_persons | Nombre de personnes exerçant un travail en lien avec l'agriculture |
| total_labour_AWU | Total des unités-travail-années (UTA) sur les exploitations (AWU en anglais) |
| nonfamily_labour_persons | Total des personnes extérieures au cercle familiale de l'exploitation |
| nonfamily_labour_AWU | Total des unités-travail-années (AWU) des personnes extérieures au cercle familiale de l'exploitation |
| managers_basic_training | Nombre d'exploitations dont l'exploitant a reçu une formation de base en agriculture |
| managers_only_practical | Nombre d'exploitations dont l'exploitant a seulement une expérience du terrain |
| managers_full_training | Nombre d'exploitations dont l'exploitant a reçu une formation complète en agriculture |
| managers_training_NA | Nombre d'exploitations non concernées par les 3 colonnes précédentes |
| farms_SO_zero | Nombre d'exploitations dont la production standard est nulle |
| farms_SO_less2000 | Nombre d'exploitations dont la production standard est inferieure à 2000 euros |
| farms_SO_2000-3999 | Nombre d'exploitations dont la production standard est comprise entre 2000 et 3999 euros |
| farms_SO_4000-7999 | Nombre d'exploitations dont la production standard est comprise entre 4000 et 7999 euros |
| farms_SO_8000-14999 | Nombre d'exploitations dont la production standard est comprise entre 8000 et 14999 euros |
| farms_SO_15000-24999 | Nombre d'exploitations dont la production standard est comprise entre 15000 et 24999 euros |
| farms_SO_25000-49999 | Nombre d'exploitations dont la production standard est comprise entre 25000 et 49999 euros |
| farms_SO_50000-99999 | Nombre d'exploitations dont la production standard est comprise entre 50000 et 99999 euros |
| farms_SO_100000-249999 | Nombre d'exploitations dont la production standard est comprise entre 100000 et 249999 euros |
| farms_SO_250000-499999 | Nombre d'exploitations dont la production standard est comprise entre 250000 et 499999 euros |
| farms_SO_500000_orover | Nombre d'exploitations dont la production standard est supérieure à 500000 euros |
Nous allons tout d'abord charger nos données dans un dataframe "df_farm", puis en visualiser un extrait :
setwd("C:/Users/gorenja/dataSciences/data")
Sys.getlocale(category="LC_ALL")
df_farm <- read.table("EuropeanAgriculture_FarmStructureIndicators_Eurostat2016.csv",
header = TRUE,
row.names=1,
sep = ",",
quote = "\"",
fill = TRUE,
comment.char = "")
head(df_farm)
farms_number used_agricultural_area_ha standard_output_EUR ...
Belgium 36890 1354250 8037986420 ...
Bulgaria 202720 4468500 3842891030 ...
Czechia 26530 3455410 13297662451 ...
Denmark 35050 2614600 10062442040 ...
Germany 276120 16715320 49249020560 ...
Estonia 16700 995100 801547060 ...
...
Dans le code ci-dessus, nous avons défini notre répertoire de travail puis chargé les données. Vous noterez que nous avons pris soin de spécifier row.names=1 afin que le pays fasse office d'index.
Exploration des données (EDA)
En termes d'analyse exploratoire, nous allons être brefs car ce n'est pas le sujet de cet article. Il nous faut cependant nous assurer de deux choses. D'une part, que toutes les colonnes soient bien numériques et, d'autre part, que nous n'avons pas de valeurs manquantes.
Commençons par nous assurer que toutes les colonnes, à l'exception du pays, sont bien numériques :
str(df_farm)
'data.frame': 28 obs. of 23 variables: $ farms_number : int 36890 202720 ... $ used_agricultural_area_ha : int 1354250 4468500 ... $ standard_output_EUR : num 8037986420 3842891030 ... $ subsistence_semisubsistence_farms: int NA 0 ... $ total_labour_persons : int 70910 439740 ... $ total_labour_AWU : int 55350 255520 ... $ nonfamily_labour_persons : int 19800 64490 ... $ nonfamily_labour_AWU : int 14810 59100 ... $ managers_basic_training : int 9940 5360 ... $ managers_only_practical : int 19100 182310 ... $ managers_full_training : int 7850 13350 ... $ managers_training_NA : int NA 260 ... $ farms_SO_zero : int 30 760 ... $ farms_SO_less2000 : int 310 105730 ... $ farms_SO_2000.3999 : int 580 35210 ... $ farms_SO_4000.7999 : int 1380 22440 ... $ farms_SO_8000.14999 : int 2410 13590 ... $ farms_SO_15000.24999 : int 2670 8450 ... $ farms_SO_25000.49999 : int 4310 6780 ... $ farms_SO_50000.99999 : int 5130 4040 ... $ farms_SO_100000.249999 : int 9010 2740 ... $ farms_SO_250000.499999 : int 7170 1480 ... $ farms_SO_500000_orover : int 3880 1510 ...
Nous avons défini le code pays comme index de chaque observation, c'est pourquoi il ne ressort pas ici. Nous constatons que l'ensemble des variables sont numériques, nous pouvons continuer.
Voyons à présent si certaines variables comptent des valeurs manquantes. Ce qui est fort probable puisque nous en apercevons déjà dans la sortie de la commande précédente.
colSums(is.na(df_farm))
farms_number used_agricultural_area_ha
0 0
total_labour_persons total_labour_AWU
0 0
managers_basic_training managers_only_practical
0 0
farms_SO_zero farms_SO_less2000
2 0
farms_SO_8000.14999 farms_SO_15000.24999
0 0
farms_SO_100000.249999 farms_SO_250000.499999
0 0
standard_output_EUR subsistence_semisubsistence_farms
1 4
nonfamily_labour_persons nonfamily_labour_AWU
2 2
managers_full_training managers_training_NA
0 17
farms_SO_2000.3999 farms_SO_4000.7999
0 0
farms_SO_25000.49999 farms_SO_50000.99999
0 0
farms_SO_500000_orover
0
6 colonnes sont concernées. Dans le cadre de cette étude de cas, nous allons nous contenter d'imputer, pour chacune de celles-ci, les valeurs manquantes par la moyenne de la colonne concernée :
NA2mean <- function(x) replace(x, is.na(x), mean(x, na.rm = TRUE))
df_farm[] <- lapply(df_farm, NA2mean)
Nous sommes prêts à présent, passons à la suite.
Justifier l'analyse en composantes principales
Comme nous l'avons dit, une ACP se base sur les corrélations linéaires entre les variables initiales. Par conséquent, il peut être pertinent de s'assurer que de tels liens existent. Pour cela, il suffit de dresser une matrice des corrélations entre les variables :
corFarm <- cor(df_farm, method = "pearson")
corrplot(corFarm, type="upper", order="hclust", tl.col="black", tl.srt=45)
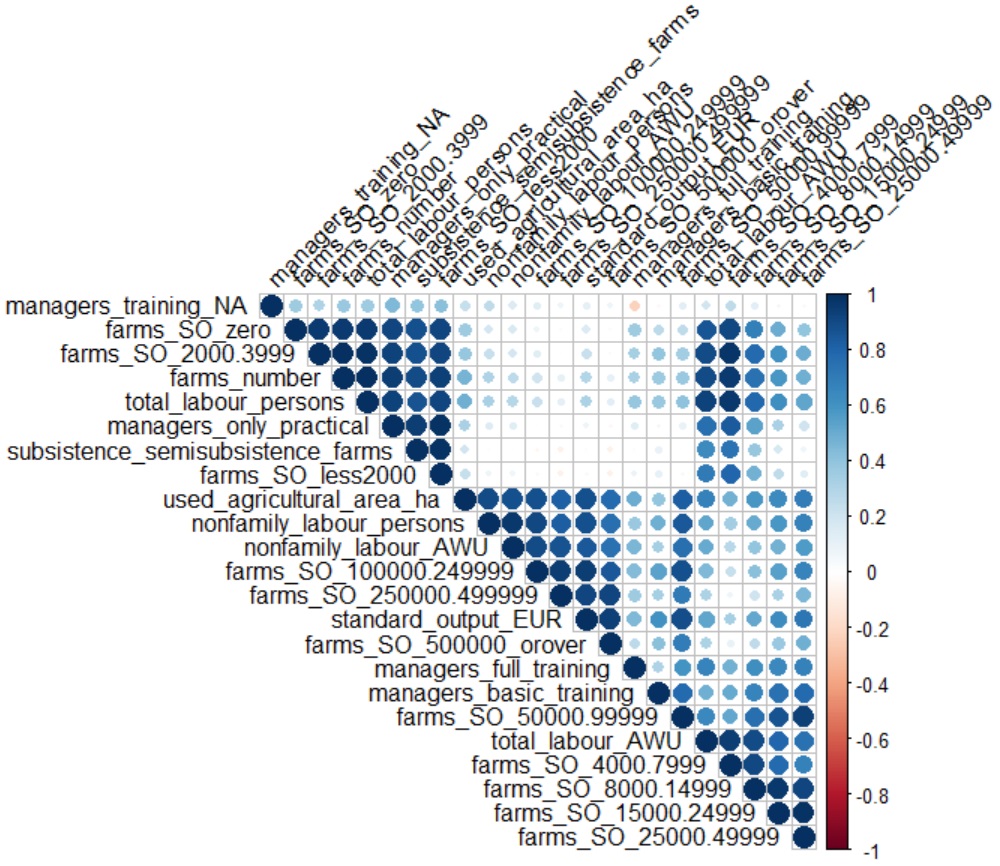
La longueur des noms de variables pénalisent un peu la lisibilité du graphique, néanmoins, nous constatons qu'certain nombre de variables peuvent être considérées comme linéairement corrélées entre elles. L'exécution d'une ACP semble pertinente sur ce jeu de données.
Détermination des composantes principales
Réaliser une ACP consiste dans un premier temps à centrer et réduire les variables, c'est à dire
à ramener leur moyenne à 0 et leur variance à 1. La matrice des corrélations est ensuite calculée.
C'est de cette matrice que l'ACP va calculer les composantes principales en déterminant puis triant
les valeurs propres (eigenvalues) et vecteurs propres (eigenvectors).
On peut définir une composante comme une combinaison linéaire des variables initiales pour laquelle
la valeur propre va constituer la quantité de variance expliquée par celle-ci.
Réalisons l'ACP via la fonction PCA de Factominer :
res <- PCA(df_farm , scale.unit=TRUE, ncp=5, graph = FALSE)
Il nous revient désormais de choisir les composantes principales générées et, pour cela, plusieurs solutions s'offrent à nous.
Choix des composantes principales
Part d'inertie expliquée
Notre objectif est de choisir un minimum de composantes expliquant un maximum d'information. Ce dernier
critère va se traduire par la part d'inertie expliquée.
Editons le tableau des valeurs propres associées à chaque composantes :
round(res$eig, 1)
eigenvalue percentage cumulative
of variance percentage
of variance
===============================================
comp 1 12.2 52.9 52.9
comp 2 6.3 27.5 80.3
comp 3 2.1 9.2 89.6
comp 4 0.9 4.1 93.7
comp 5 0.7 2.9 96.6
comp 6 0.3 1.3 97.9
comp 7 0.2 1.1 99.0
comp 8 0.1 0.4 99.4
comp 9 0.1 0.3 99.7
comp 10 0.0 0.2 99.9
comp 11 0.0 0.0 99.9
comp 12 0.0 0.0 99.9
comp 13 0.0 0.0 100.0
comp 14 0.0 0.0 100.0
comp 15 0.0 0.0 100.0
comp 16 0.0 0.0 100.0
comp 17 0.0 0.0 100.0
comp 18 0.0 0.0 100.0
comp 19 0.0 0.0 100.0
comp 20 0.0 0.0 100.0
comp 21 0.0 0.0 100.0
comp 22 0.0 0.0 100.0
comp 23 0.0 0.0 100.0
Nous pouvons constater sur le tableau ci-dessus que les 3 premières composantes
résument 89.6% de la dispersion. 52.9% de l’inertie est récupérée par la première
dimension, 27.5% par la seconde puis 9.2% par la troisième.
Choisir, par conséquent, les 3 premières composantes peut se révéler pertinent. Il
existe, cependant, une méthode complémentaire : le critère de Kaiser.
Critère de Kaiser
Nous avons réduit nos variables lors de l'exécution de l'ACP, leur variance respective est donc égale à 1. Le critère de Kaiser va consister à ne retenir que les composantes dont la variance est supérieure à 1 car celles-ci apportent plus d'information que les variables initiales.
Si nous nous basons sur le tableau des valeurs propres dressé précédemment, nous constatons
que le critère de Kaiser conforte notre choix initial de ne retenir que les 3 premières
composantes.
Nous allons enfin évoquer un troisième critère, celui qui consiste à analyser les différences
entre les valeurs propres, appelé plus communément le critère du coude.
Critère du coude
Nous nous basons ici sur le diagramme des éboulis qui va venir dresser l'histogramme des valeurs propres. Notre objectif est alors d'observer une cassure, un coude, et de ne retenir que les composantes situées en amont.
eigenvalues <- res$eig
barplot(eigenvalues[, 2], names.arg=1:nrow(eigenvalues),
main = "Diagramme des éboulis",
xlab = "Composantes principales",
ylab = "Pourcentages de variance",
col ="steelblue")
lines(x = 1:nrow(eigenvalues), eigenvalues[, 2], type="b", pch=19, col = "red")
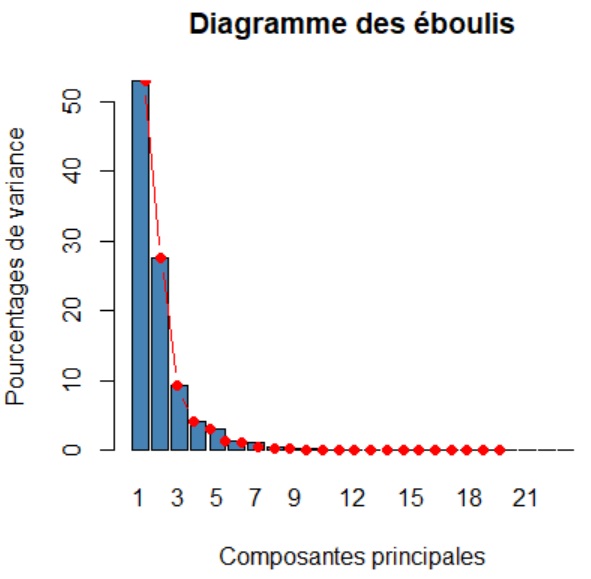
Sur le diagramme ci-dessus nous pouvons situer le coude au niveau de la 4e composante dans la mesure où la différence entre les variances des composantes 4 et 5 s'atténue nettement par rapport aux composantes précédentes. Là encore, ce critère nous incite à ne retenir que les 3 premières composantes.
Notre choix étant arrêté, il est temps de passer à l'interprétation.
Interprétation des composantes principales
Une composante principale est une combinaison linéaire des variables initiales. Interpréter une composante n'est pas aussi aisé qu'interpréter une variable dont on connait la signification. Afin de nous y aider, nous allons analyser un premier graphique, le graph des variables. Celui-ci porte sur un duo de composantes et représente les corrélations de chacune des variables initiales avec celles-ci. Analysons tout d'abord le graph des variables du couple de composantes 1 et 2 (également appelé plan principal) :
print(plot.PCA(res, axes=c(1, 2), choix="var", new.plot=TRUE,
col.var="black", col.quanti.sup="blue",
label=c("var", "quanti.sup"), lim.cos2.var=0))
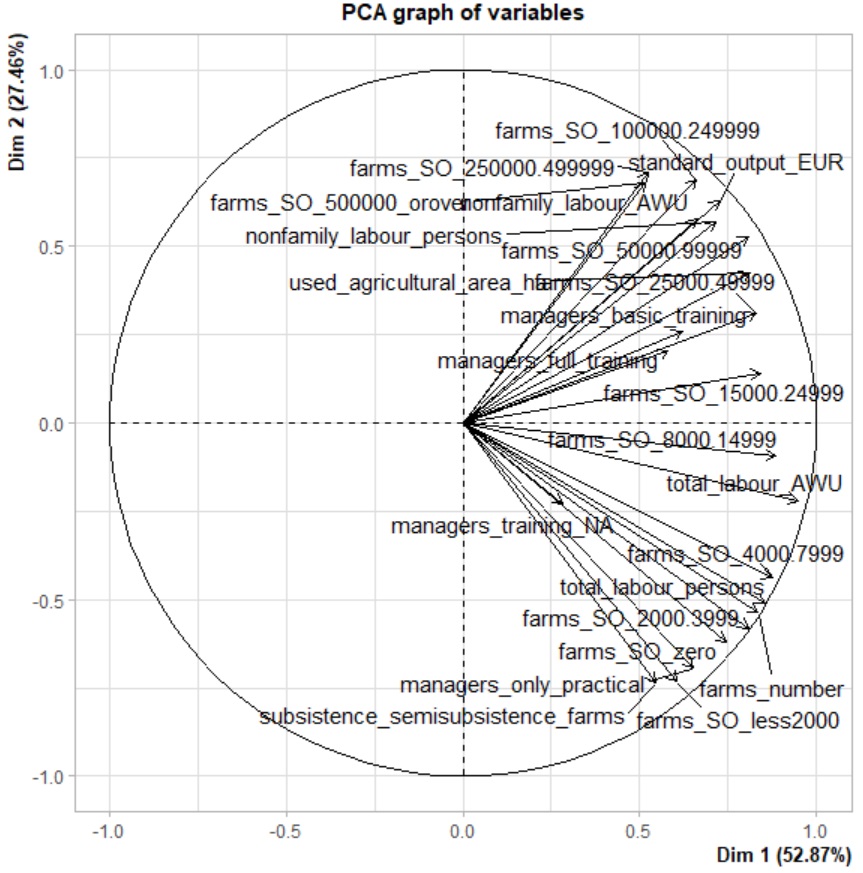
Le graph est composé de deux axes, la composante 1 (Dim 1) en abscisses et la composante 2 (Dim 2) en ordonnées.
Chaque variable initiale est matérialisée par une flèche pour laquelle il convient de regarder la longueur et le sens, ou
plutôt l’angle de la pointe par rapport à la composante analysée. Cette flèche symbolise le lien de corrélation entre
la variable et la composante et donc, sa contribution.
L'analyse du graphe des variables peut également s'appuyer sur le tableau des corrélations variables / composantes (nommées
également dimensions, comme vous l'aurez compris). Dressons ce tableau pour les 3 premières composantes :
res$var$cor
Dim.1 Dim.2 Dim.3
farms_number 0.8352687 -0.53707189 0.08685494
used_agricultural_area_ha 0.8121516 0.42646089 0.25979852
standard_output_EUR 0.7275699 0.62896387 0.16281423
subsistence_semisubsistence_farms 0.5446950 -0.73683967 0.31622551
total_labour_persons 0.8552822 -0.51158885 0.04565159
total_labour_AWU 0.9487246 -0.21868042 -0.10356751
nonfamily_labour_persons 0.7165103 0.56806564 0.24781709
nonfamily_labour_AWU 0.6622702 0.57751949 0.31237255
managers_basic_training 0.6209246 0.25786835 -0.40918440
managers_only_practical 0.6524379 -0.69391350 0.27371155
managers_full_training 0.5814797 0.20312351 -0.42864694
managers_training_NA 0.2822331 -0.23080084 0.55494409
farms_SO_zero 0.7453829 -0.62090373 0.04017123
farms_SO_less2000 0.6055462 -0.73249789 0.28048520
farms_SO_2000.3999 0.8075679 -0.58078587 -0.03303884
farms_SO_4000.7999 0.8765938 -0.43779972 -0.18172821
farms_SO_8000.14999 0.8874045 -0.09382263 -0.40774634
farms_SO_15000.24999 0.8436496 0.14227566 -0.46845552
farms_SO_25000.49999 0.8301990 0.30889337 -0.42870679
farms_SO_50000.99999 0.8083235 0.52738057 -0.17845784
farms_SO_100000.249999 0.6604612 0.68962582 0.21418951
farms_SO_250000.499999 0.5250932 0.71043847 0.38969428
farms_SO_500000_orover 0.5171646 0.68120674 0.32090269
Nous voyons que l'ensemble des variables sont corrélées positivement avec la composante 1. Les variables qui apparaissent comme étant étroitement liées à celle-ci sont essentiellement le nombre des exploitations, la surface exploitée et le nombre de personnes travaillant dans le domaine de l'agriculture. Par ailleurs, la composante 1 semble se concentrer en grande partie sur les exploitations de taille moyenne (dont la production standard est comprise entre 2000 et 99999 euros).
La seconde composante semble porter sur les exploitations hors normes, très petites (production standard inferieure à 2000 euros) ou au contraire très grandes (production standard supérieure à 100000 euros). Par ailleurs, cette composante s'intéresse à la semi-subsistance et à l'apprentissage par la pratique des exploitants. Ceci semble logique puisqu’à priori très corrélé aux exploitations de petites tailles.
Analysons à présent le graph des variables des composantes 1 et 3 afin de caractériser la 3e composante :
print(plot.PCA(res, axes=c(1, 3), choix="var", new.plot=TRUE,
col.var="black", col.quanti.sup="blue",
label=c("var", "quanti.sup"), lim.cos2.var=0))
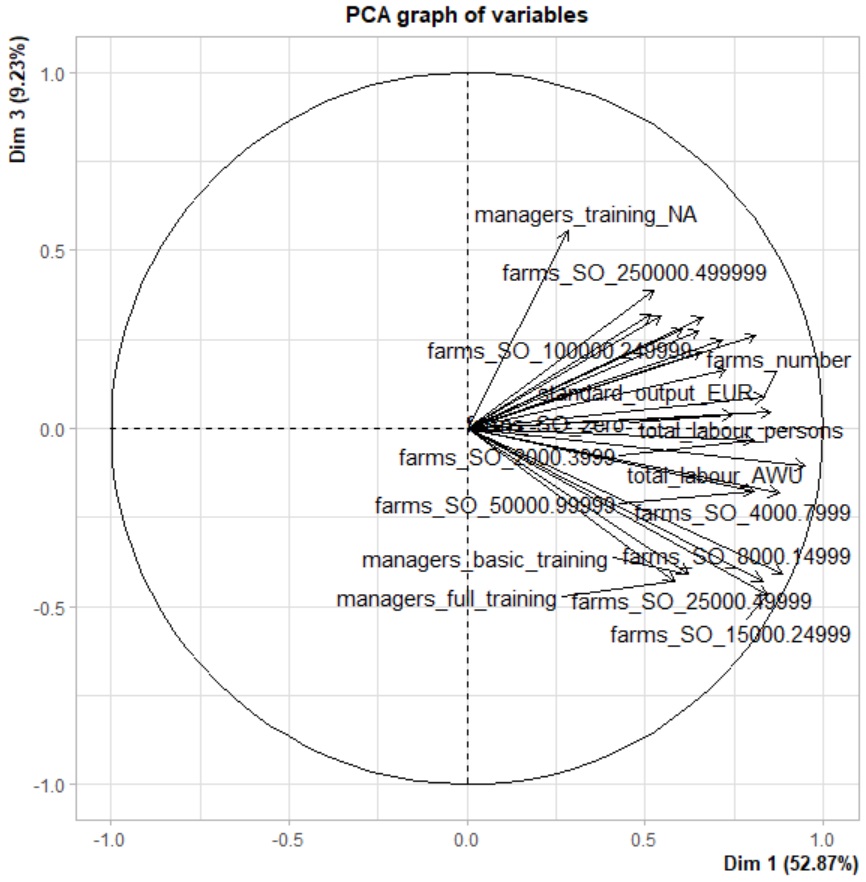
Les variables semblent toutes relativement éloignées de cette composante à l'exception du nombre d'exploitations dont l'apprentissage de l'exploitant n'a pas pu être établi clairement. Par ailleurs, à l'inverse de la seconde composante, cette 3e dimension est plutôt associée, via une relation négative, à l'apprentissage basic ou complet de l'exploitant.
Nous avons brièvement caractérisé nos composantes. Nous sommes à présent en mesure d'expliquer ce sur quoi elles portent et pouvons passer à l'étape suivante : l'analyse des individus (dans notre cas les pays).
Interprétation des individus
L'interprétation des individus, donc des pays, va consister à mesurer la qualité de représentation de ces derniers sur chacune des 3 composantes. Ensuite il conviendra d'analyser leur contribution respective.
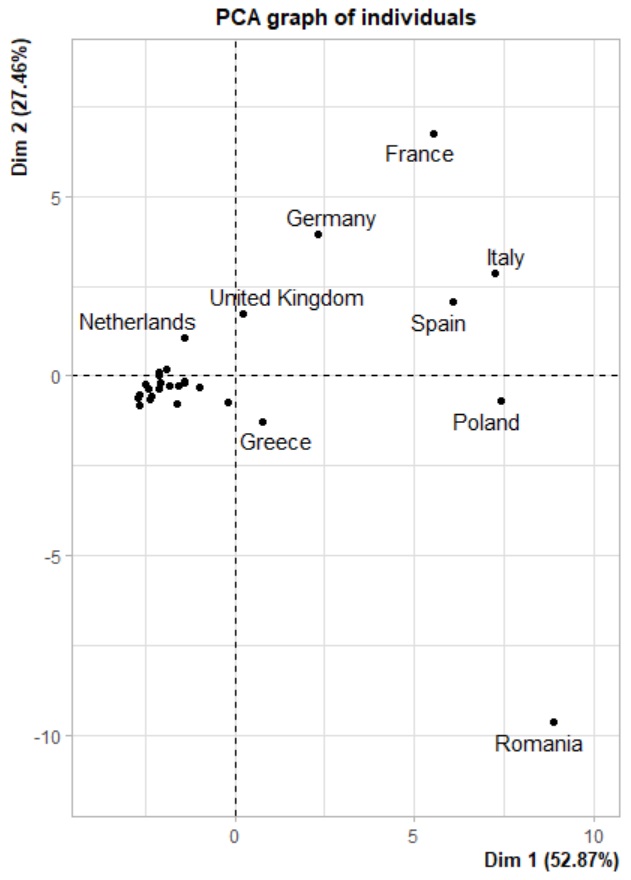
A l'instar des variables, le principal vecteur d'analyse va être un graphique, le graph des individus. Dressons celui du plan principal (composantes 1 et 2) avant de revenir sur la qualité de représentation d'abord et la contribution ensuite :
print(plot.PCA(res, axes=c(1, 2), choix="ind", habillage="none",
col.ind="black", col.ind.sup="blue", col.quali="magenta",
label=c("ind", "ind.sup", "quali"),new.plot=TRUE))
Qualité de représentation des pays
La qualité de représentation d'un individu sur un axe se mesure par le rapport entre la distance à l'origine
de cet individu avant puis après projection. Ce rapport est appelé cos2. D'une manière générale, on pourra
admettre qu'un individu est bien représenté :
- sur l'axe 1 si le rapport cos2 est supérieur à 0.5
- sur l'axe 2 si le rapport cos2 est supérieur à 0.25
- sur l'axe 3 si le rapport cos2 est supérieur à 0.15
Bien entendu, seuls les individus bien représentés seront interprétés.
Dressons la liste des rapports cos2 pour les 3 composantes :
costab <- res$ind$cos2
tmp <- costab[, "Dim.1", drop = FALSE]
df <- data.frame(round(tmp[,1], 2))
names(df)[1] <- "Dim1"
head(df[order(-df$Dim1), , drop = FALSE], 30)
tmp <- costab[, "Dim.2", drop = FALSE]
df <- data.frame(round(tmp[,1], 2))
names(df)[1] <- "Dim2"
head(df[order(-df$Dim2), , drop = FALSE], 30)
tmp <- costab[, "Dim.3", drop = FALSE]
df <- data.frame(round(tmp[,1], 2))
names(df)[1] <- "Dim3"
head(df[order(-df$Dim3), , drop = FALSE], 30)
Dim1 Dim2 Dim3
===============================================================
Slovakia 0.96 Germany 0.60 Greece 0.39
Sweden 0.96 Romania 0.51 Poland 0.24
Estonia 0.95 France 0.50 Italy 0.12
Cyprus 0.93 United Kingdom 0.41 Netherlands 0.12
Latvia 0.92 Hungary 0.28 Germany 0.11
Denmark 0.91 Greece 0.18 France 0.11
Finland 0.91 Netherlands 0.17 Portugal 0.08
Belgium 0.89 Lithuania 0.15 Ireland 0.07
Luxembourg 0.88 Italy 0.10 Croatia 0.05
Slovenia 0.88 Spain 0.08 Romania 0.05
Malta 0.87 Luxembourg 0.08 Hungary 0.04
Czechia 0.82 Slovenia 0.07 United Kingdom 0.04
Ireland 0.68 Cyprus 0.05 Czechia 0.03
Spain 0.67 Latvia 0.05 Belgium 0.02
Lithuania 0.66 Portugal 0.05 Bulgaria 0.02
Poland 0.65 Estonia 0.04 Spain 0.02
Italy 0.64 Finland 0.03 Slovenia 0.02
Bulgaria 0.63 Bulgaria 0.02 Denmark 0.01
Croatia 0.58 Slovakia 0.02 Lithuania 0.01
Portugal 0.51 Czechia 0.01 Austria 0.01
Romania 0.43 Ireland 0.01 Estonia 0.00
France 0.34 Croatia 0.01 Cyprus 0.00
Netherlands 0.29 Malta 0.01 Latvia 0.00
Austria 0.28 Austria 0.01 Luxembourg 0.00
Germany 0.21 Poland 0.01 Malta 0.00
Greece 0.06 Sweden 0.01 Slovakia 0.00
Hungary 0.02 Belgium 0.00 Finland 0.00
United Kingdom 0.01 Denmark 0.00 Sweden 0.00
Nous constatons que la plupart des pays sont bien représentés sur l'axe 1, à l'exception de 8 d'entre eux dont la France, l'Allemagne, la Roumanie, la Hongrie et le Royaume-Uni. Ce sont d'ailleurs ces derniers que nous retrouvons comme étant les mieux représentés sur le second axe. Cela signifie que ces 5 pays devront être analysés sur la base de l'interprétation que nous avons fait de l'axe 2, le reste des pays selon les variables associées a l'axe 1.
Nous pouvons formuler quelques commentaires sur la base des informations que nous avons désormais. Ainsi, à la
vue du graph des individus, il semble que la Pologne, l'Espagne et l'Italie se détachent de leurs voisins sur
la surface agricole exploitée rapportée au nombre d'exploitations de tailles moyennes ainsi qu'au personnel œuvrant
dans le secteur agricole.
Par ailleurs, la France et la Roumanie semblent s'opposer totalement en ce qui concerne le nombre de petites
exploitations que l'on associe à une pratique importante de semi-subsistance et un apprentissage des exploitants
par la pratique. Il suffira pour s'en convaincre de comparer les chiffres pour ces 2 pays sur les variables initiales.
Sur la 3e composante, seule une interprétation de la Grèce et de la Pologne sera pertinente. Dressons le graph des individus sur le couple de composantes 1 et 3 :
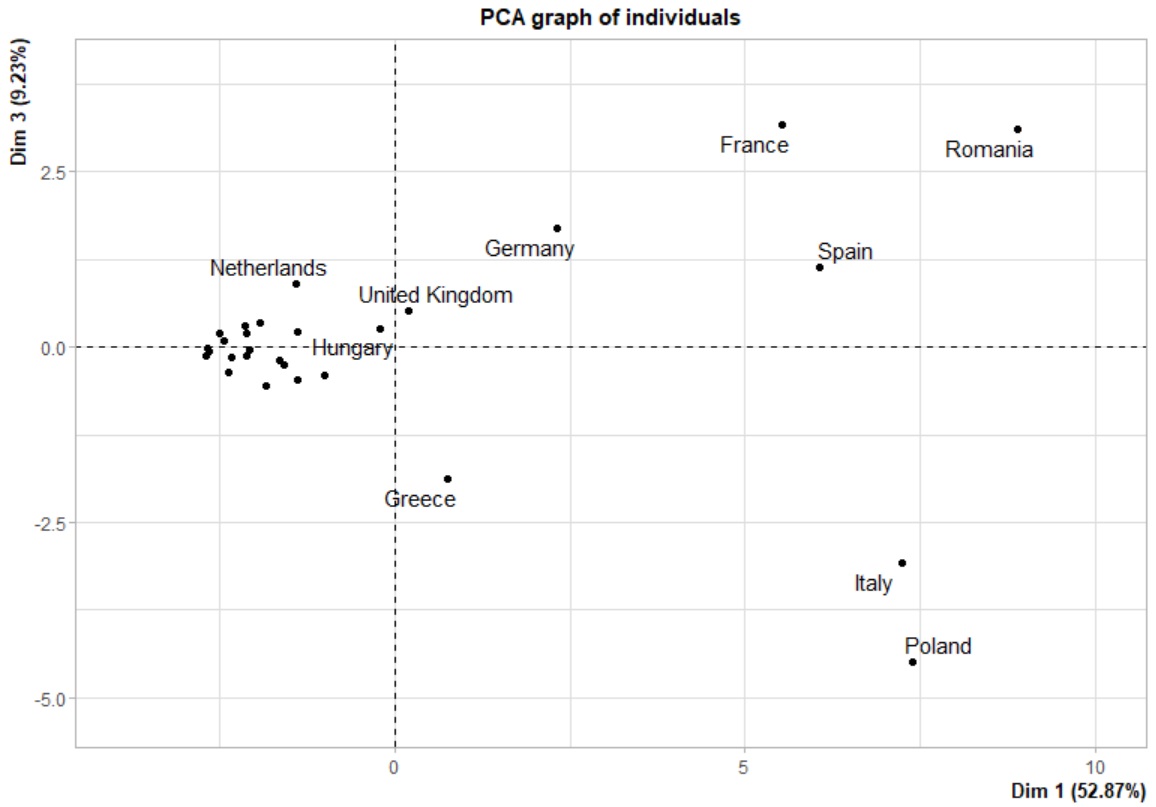
Rappelons que la 3e composante est liée à une certaine incertitude quant à la façon dont l'exploitant a appris son métier. La Pologne comme la Grèce sont liées à la composante 3 selon un sens identique. On constate cependant que la Grèce est plus proche de l'origine, ce qui peut sous-entendre, soit que le recensement a été plus difficile pour la Pologne, soit que l'offre de formation agricole est plus restreinte.
Voyons à présent la contribution des individus.
Contribution des individus
Evaluer la contribution d'un individu à un axe sert principalement à dégager les fortes contributions. Ces dernières
peuvent en effet modifier l'analyse, comme un outlier pourrait le faire par exemple en faussant une relation de
corrélation linéaire. On entend par forte contribution une contribution supérieure à 1/n * 100, ou n
représente le nombre d'individus. Il convient pour ces fortes contributions de les spécifier à l'ACP comme
individus supplémentaires.
Dressons, pour illustrer nos propos, la contribution des individus à l'axe 1 :
contrib <- res$ind$contrib / 12.2
tmp <- contrib[,"Dim.1", drop = FALSE]
df <- data.frame(tmp[,1])
names(df)[1] <- "Dim1"
df <- df[order(-df$Dim1), , drop = FALSE]
df
par(mai=c(0.4,2,0.4,0.5))
barplot(df[, 1], names.arg=rownames(df), horiz=TRUE,
main = "Contribution des pays au premier axe",
col ="steelblue",las=1)
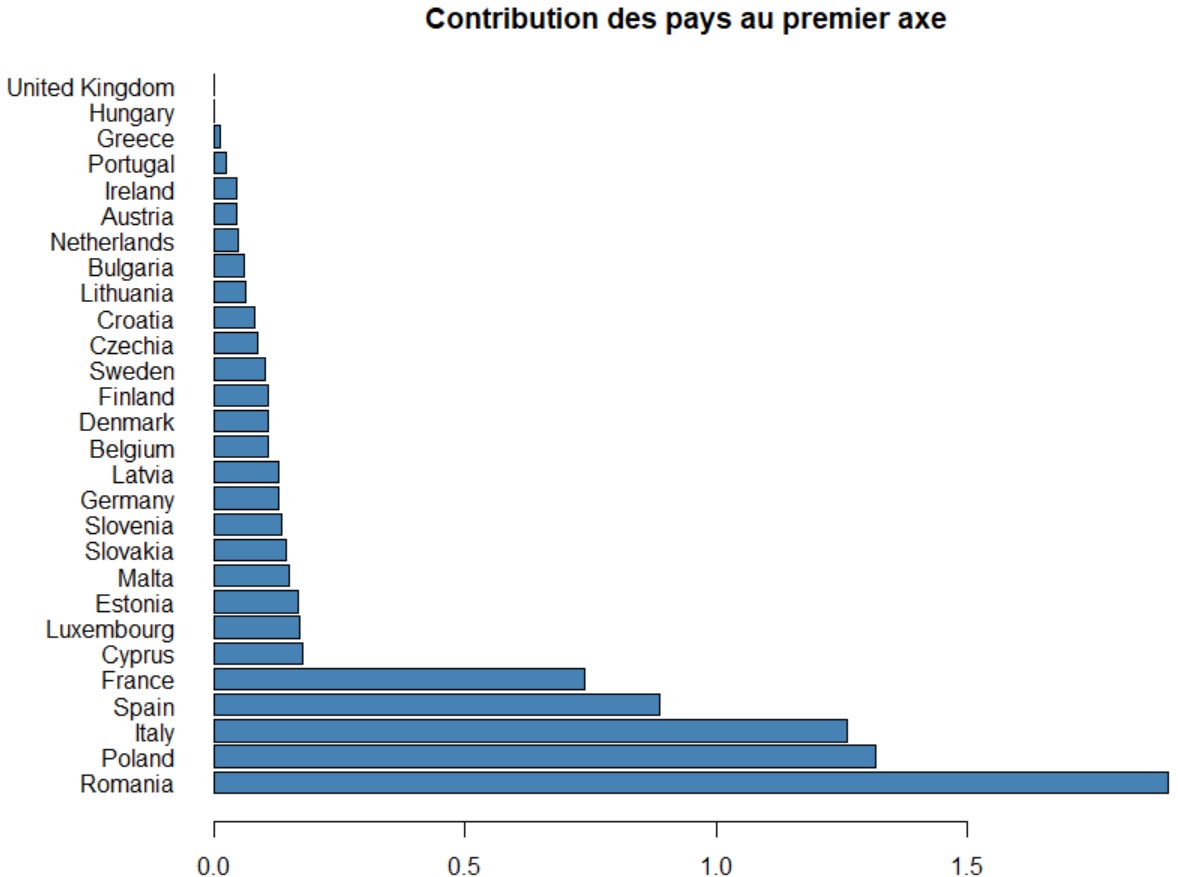
Vous noterez que nous avons divisé la contribution retournée par R par la valeur propre de la dimension étudiée (ici l'axe 1).
Credits
Informations legales et copyright concernant les donnees : Legal Notice.
Retrouvez dans la rubrique "Nos datasets" toutes les données dont vous aurez besoin pour tester et pratiquer !

