Matrice de corrélation sous R
Dressez et paramétrer rapidement un corrélogramme avec la librairie corrplot
Lorsqu'il s'agit de représenter graphiquement les corrélations entre plusieurs variables d'un
set de données, le corrélogramme, souvent résumé à sa forme matricielle, est l'option la
plus efficace. Cette forme de représentation permet en effet de traduire facilement la force
des relations qui unissent les variables entre elles.
Nous allons dans cet article nous pencher sur l'utilisation de la librairie corrplot. Sachez cependant
qu'il en existe beaucoup d'autres.
Données de travail
Pour illustrer nos propos, nous allons travailler avec un dataset de 150 transactions
immobilières, pour lesquelles nous disposons d'un certain nombre d'informations comme le nombre de chambres,
de salles de bain et de places de stationnement, mais également de la surface, de l'étage ainsi que du nombre
d'étages total de l'immeuble. Enfin nous disposons de 2 variables catégorielles, la présence d'un balcon et le
type de chauffage.
Les données brutes de ce dataset sont disponibles sur Gorenja.com
ici.
Chargeons nos données dans un dataframe "df_appart" et visualisons un extrait :
df_appart <- read.table("appartements.csv", header = TRUE,
sep = ";",
quote = "\"",
fill = TRUE,
comment.char = "")
head(df_appart)
bien chb sdb surface parking balcon chauffage etage etage_imm prix 1 REF23978 2 1 30 1 non gaz 1 5 99000 2 REF35989 2 1 30 2 non electrique 4 7 158000 3 REF34600 2 1 53 1 non gaz 10 12 348000 4 REF24544 1 1 33 1 oui gaz 9 11 120000 5 REF30844 3 1 44 1 oui gaz 10 11 195000
Le dataset est composé de 2 variables catégorielles que sont la présence d'un balcon et le type de chauffage. Pour être exhaustif dans notre étude des corrélations il nous faudrait prendre en compte ces 2 variables en procédant au préalable à un codage disjonctif complet (one hot encoding) de celles-ci. Nous traiterons ce point dans un article à venir, aussi nous allons, pour l'heure, nous contenter d'étudier les corrélations des variables quantitatives.
Nous allons exclure du dataset les variables non numériques à présent :
df_appart <- df_appart[names(df_appart)[sapply(df_appart, is.numeric)]]
head(df_appart)
chb sdb surface parking etage etage_imm prix 1 2 1 30 1 1 5 99000 2 2 1 30 2 4 7 158000 3 2 1 53 1 10 12 348000 4 1 1 33 1 9 11 120000 5 3 1 44 1 10 11 195000
Installation et import de la librairie corrplot
Nous installons à présent (pour ceux qui ne l'ont pas déjà) la librairie corrplot puis la chargeons.
install.packages("corrplot")
library(corrplot)
Matrice de correlation
Le corrélogramme est réalisé sur la base d'une matrice de corrélation, aussi il nous faut la générer
avant de procéder au rendu graphique.
La fonction cor de R va nous permettre de calculer la coefficient de corrélation entre 2 variables ou bien,
comme c'est notre cas, entre les variables, 2 a 2, qui constituent un set de données. Cette fonction donne
la possibilité de calculer le coefficient de corrélation linéaire de Pearson ou encore les corrélations de rangs de
Kendall ou Spearman.
Nous allons opter pour le coefficient de Pearson :
corr <- cor(df_appart, method="pearson")
round(corr, 2)
chb sdb surface parking etage etage_imm prix
chb 1.00 0.30 0.80 0.27 -0.02 0.03 0.68
sdb 0.30 1.00 0.14 0.03 -0.12 0.03 0.04
surface 0.80 0.14 1.00 0.24 -0.03 -0.04 0.88
parking 0.27 0.03 0.24 1.00 0.10 0.03 0.23
etage -0.02 -0.12 -0.03 0.10 1.00 0.71 0.12
etage_imm 0.03 0.03 -0.04 0.03 0.71 1.00 -0.08
prix 0.68 0.04 0.88 0.23 0.12 -0.08 1.00
Correlogramme
La matrice de corrélation étant générée, il ne nous reste plus qu'à la représenter graphiquement. L'opération
va s'effectuer via la fonction corrplot. Dans une utilisation de base, celle-ci a 2 paramètres principaux.
Tout d'abord, la méthode de représentation (method) qui peux prendre comme valeurs circle, color, shade, square,
ellipse, number ou pie. Certaines représentations sont plus lisibles que d'autres en fonction des données. Il convient
de faire de tests.
Ensuite, le type de structure (type) : full (par défaut), upper et lower. Ces valeurs afficheront respectivement
la matrice complète ou simplement le triangle supérieur ou inférieur.
Ci-dessous le résultat de 2 représentations possibles de notre matrice :
corrplot(corr, method="circle")
corrplot(corr, method="color", type="upper")
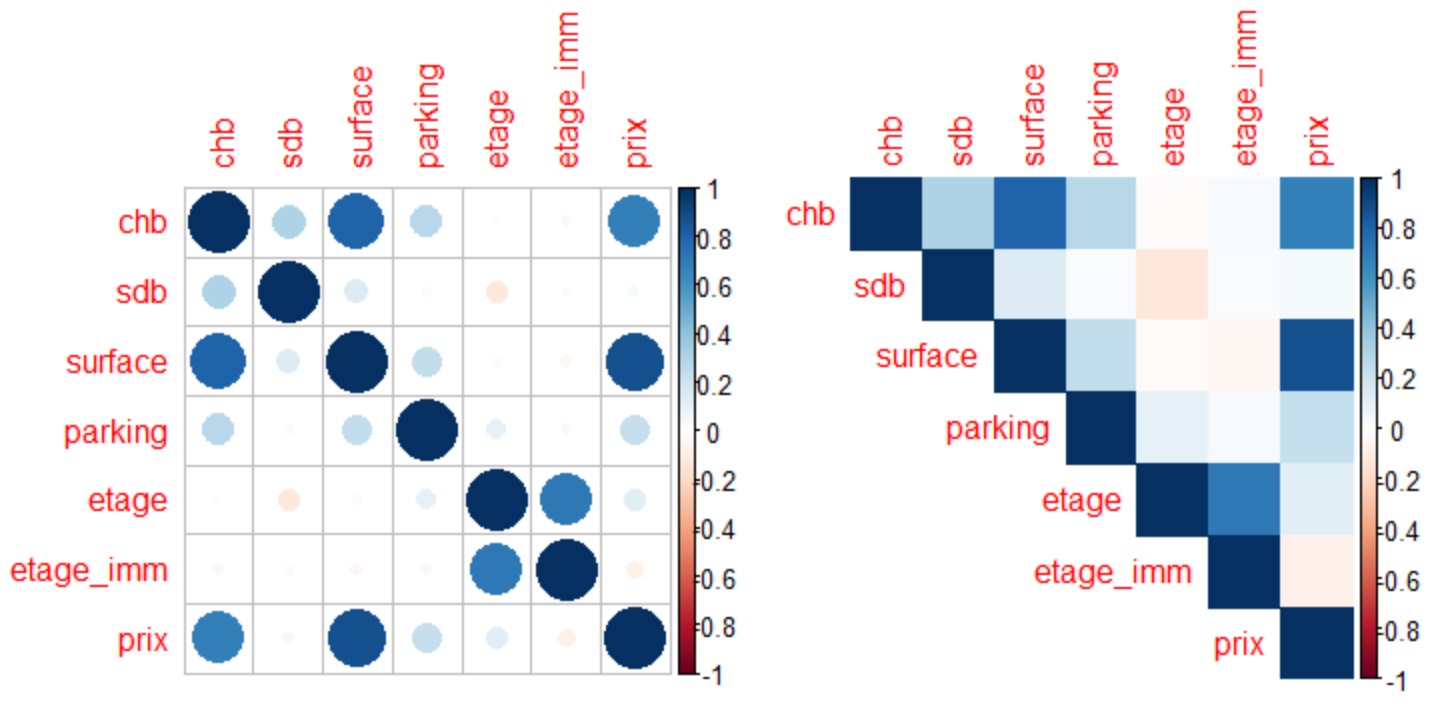
Dans notre cas, la représentation de droite semble plus lisible. Le prix de ventre semble être corrélé avec la surface d'abord puis le nombre de chambres ensuite. Il est possible d'avoir un sentiment plus immédiat de la hiérarchie via le paramètre hclust.
Ordonner la matrice selon l'intensité du lien
Le paramètre hclust va en effet nous permettre de hiérarchiser les variables en fonction de l'intensité du
lien qui les unie.
Nous en profitons, par ailleurs, pour colorer les noms de variables et les incliner de 45 degrés via les
paramètres tl.col et tl.srt
Voici le résultat :
corrplot(corr, method="color", type="upper",
order="hclust",
tl.col="orange", tl.srt=45)
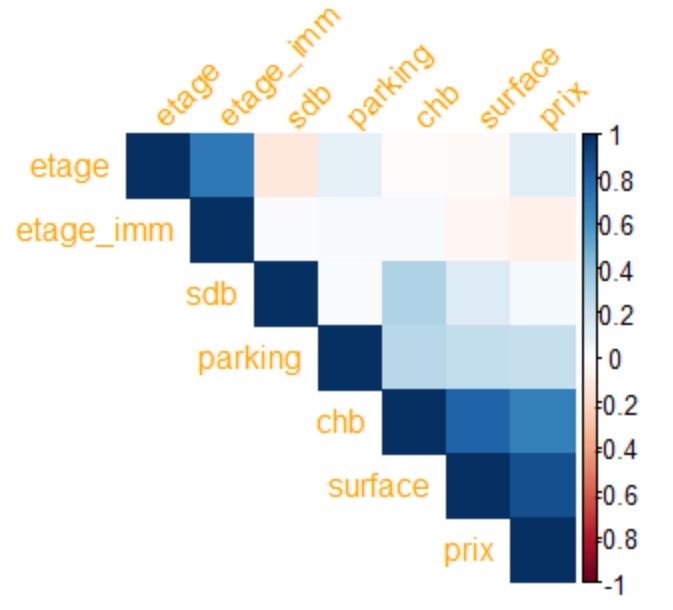
Retrouvez dans la rubrique "Nos datasets" toutes les données dont vous aurez besoin pour tester et pratiquer !

