Régression linéaire sous R
Ajuster linéairement une série statistique sous R
La régression linéaire, dans son principe, est relativement simple à appréhender puisqu'il
s'agit, visuellement parlant, de faire passer une droite au plus près des points qui forment
un nuage. C'est donc un ajustement linéaire, au cours duquel une variable est expliquée
au moyen d'une autre, d'où les termes respectifs de variable expliquée et variable explicative.
Un exemple classique consiste à vouloir exprimer le prix d'un appartement en fonction de sa
superficie. Comme l'illustre le nuage de points ci-dessous, les 2 variables prix de vente et superficie,
respectivement variable expliquée en abscisse et variable explicative en ordonnée, présentent de toute évidence
une relation de corrélation linéaire.
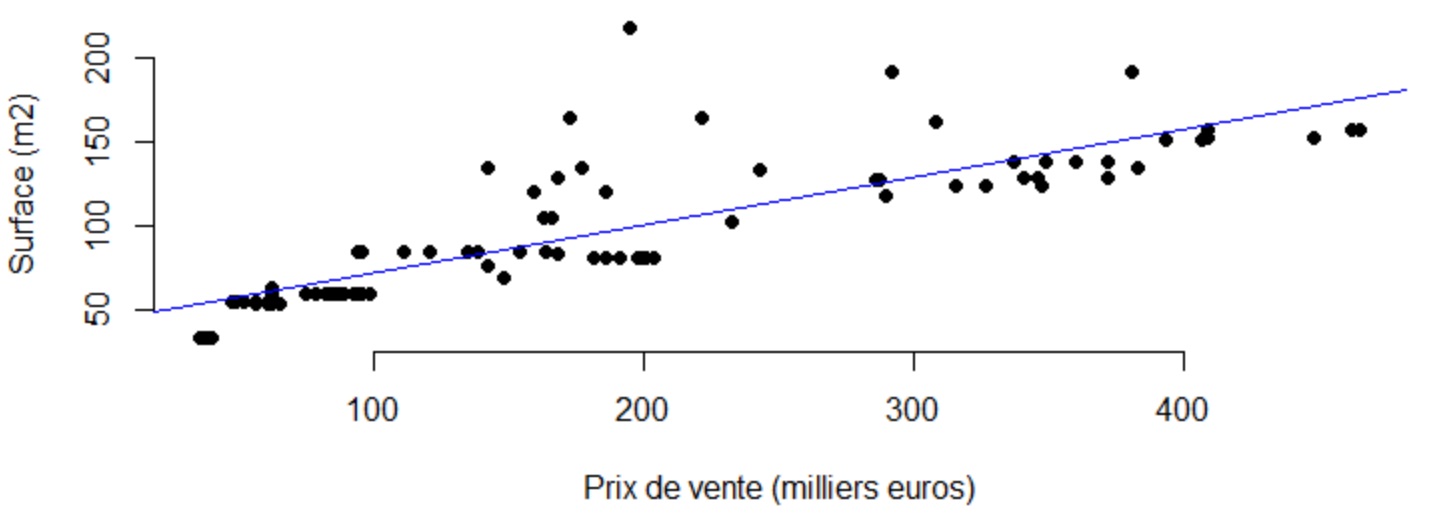
La droite d'ajustement linéaire, en bleu sur le graphique, vient matérialiser le consensus qui, a une superficie, associe un prix moyen de vente. L'intérêt d'une telle démarche réside bien entendu dans le fait, qu'avec cette relation, nous tenons un modèle nous permettant d'estimer un bien.
Régression simple vs multiple
L'exemple du prix de vente des appartements ci-dessus est une régression simple, dans la mesure où il n'y a qu'une seule variable explicative, en l'occurrence la superficie. Nous pourrions vouloir estimer le prix de vente sur la base d'autres critères comme le nombre de pièces par exemple. Nous parlons alors de régression multiple. Le principe est le même que celui de la régression simple. Par ailleurs les variables explicatives doivent être indépendantes les unes des autres.
L'objet de cet article est d'implémenter une régression linéaire sous R. Nous allons le faire manuellement puis comparer nos résultats avec la fonction lm (linear model) de R.
Données de travail
Nous disposons d'un dataset listant les scores d'audimat (en millions de téléspectateurs) sur une agglomération
donnée entre le 1er janvier 2010 et le 30 septembre 2016. Les relevés sont quotidiens et accompagnés de la température
extérieure ainsi que des précipitations constatées le jour de l'observation.
Notre mission va consister à établir un modèle de régression linéaire multiple afin d'expliquer l'audimat en fonction
de la température, des précipitations et du jour de la semaine.
Une fois le modèle créé, nous tenterons de prédire l'audimat pour la période allant du 1er au 10 octobre 2016, pour
laquelle nous disposons uniquement des températures et précipitations.
Commençons par charger nos données et voir à quoi elles ressemblent :
df_audimat <- read.table("audimat.csv", header = TRUE,
sep = ",",
quote = "\"",
fill = TRUE,
comment.char = "")
#Nous convertissons la date en format Date
df_audimat[['date']] <- as.Date(df_audimat[['date']], format='%Y-%m-%d')
head(df_audimat)
date jour temperature precipitation telespectateurs
1 2010-01-01 vendredi 7.2 3.4 48.33333
2 2010-01-02 samedi 10.9 0.8 42.33333
3 2010-01-03 dimanche 11.0 0.2 44.00000
4 2010-01-04 lundi 6.1 2.4 40.00000
5 2010-01-05 mardi 2.0 0.6 49.00000
6 2010-01-06 mercredi 0.6 1.2 35.33333
Modélisation
Commençons par évoquer notre fonction perte. Cette fonction est indispensable dans un
modèle puisqu'elle va nous permettre de mesurer l'écart (le résidu) entre une prédiction et la
valeur réelle, donc évaluer la qualité du modèle. L'objectif est de minimiser
la fonction perte.
La perte généralement associée a une régression linéaire est l'erreur quadratique
moyenne. Il s'agit donc de la moyenne de la différence quadratique (càd élevée au carré)
entre la prédiction d'un modèle et la valeur réelle. Le fait de prendre la différence
quadratique permet d'éviter une compensation entre les résidus positifs et négatifs.
L'estimateur qui permet de minimiser notre fonction perte est l'estimateur des moindres
carrés ordinaires (MCO).
Soit y un vecteur de taille n des valeurs prises par la variable expliquée
Soit ŷ un vecteur de taille n des valeurs prédites de la variable expliquée
Soit x une matrice de taille n X p des valeurs prises par les p variables explicatives
Soit x' la matrice transposée de x
On a, sous forme matricielle, le calcul ci-dessous de l'estimateur et de l'erreur quadratique :
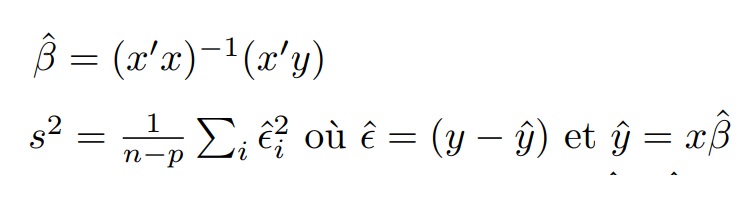
Traduisons cela sous R désormais.
Le calcul de la matrice des coefficients estimés (hat_beta), tout d'abord, peut être implémenté ainsi :
p1 <- solve(t(x)%*%x)
p2 <- t(x)%*%y
hat_beta <- p1%*%p2
Les calculs des résidus (residuals) et de l'erreur quadratique moyenne (sigma2) peuvent être implémentés ainsi :
y_pred <- x%*%hat_beta
residuals <- y - y_pred
sigma2 <- sum(residuals**2)/(nrow(x)-ncol(x))
Tests statistiques sur les paramètres
La problématique sous-jacente aux tests statistiques sur les paramètres est de savoir si une variable X explicative a significativement une influence sur la variable expliquée Y. Cela revient à émettre une hypothèse nulle : "le coefficient associé a X vaut 0, aucune influence donc" contre son alternative : "le coefficient associé a X diverge de 0". Le test associé est un test de Student et peut se calculer ainsi :

Sous R, l'implémentation associée :
t_value_beta <- hat_beta/sqrt(diag(sigma2*solve(t(x)%*%x)))
Notre fonction de régression
Il ne nous reste plus qu'à compiler le tout pour obtenir notre fonction finale de régression
linéaire (reg_lin). Cette fonction prend en entrée un vecteur y des valeurs cibles (notre variable
expliquée) et une matrice x des variables explicatives.
Vous constaterez que nous nous assurons que nous avons bien autant d'observations (nombre de lignes
de x) que de valeurs cibles (longueur de y). Par ailleurs nous retournons une liste des vecteurs et matrices
calculés, à savoir les coefficients estimés, l'erreur quadratique, les valeurs de test ainsi que les résidus.
reg_lin <- function(y, x){
stopifnot(is.vector(y) & length(y)==nrow(x))
#Détermination de la matrice des coefficients "hat_beta"
p1 <- solve(t(x)%*%x)
p2 <- t(x)%*%y
hat_beta <- p1%*%p2
#Calcul de l'erreur quadratique moyenne sigma2 et des résidus
y_pred <- x%*%hat_beta
residuals <- y - y_pred
sigma2 <- sum(residuals**2)/(nrow(x)-ncol(x))
#Calcul des statistiques de test
t_value_beta <- hat_beta/sqrt(diag(sigma2*solve(t(x)%*%x)))
return(list(hat_beta, sigma2, t_value_beta, residuals))
}
Préparation des données
Revenons désormais à notre jeu de données. En termes de préparation, nous allons procéder à trois opérations de base :
- nous procédons à un codage disjonctif (one hot encoding) des jours de la semaine, afin de transformer
cette variable qualitative en variables booléennes factices,
- nous ajoutons une colonne intercept. L'intercept représente l'estimation que fait un modèle lorsque toutes
les variables explicatives sont à zéro. Il s'agit, en d'autres termes, de l'ordonnée à l'origine,
- enfin, nous conservons uniquement les variables explicatives qui nous intéressent, nous enlevons la date,
le jour devenu inutile, ainsi que le dimanche. Une explication simple à ce dernier point :il y a 7 jours dans la semaine, le codage disjonctif complet
a donc créé 7 variables dites factices. Or la septième apporte une information redondante dans la mesure ou
une observation n'ayant trait à aucun des 6 premiers jours est forcément associée au 7e. Il convient donc
d'encoder en k-1 variables binaires, sous peine de soulever une méchante erreur de type : "system is computationally
singular: reciprocal condition number = ......
preprocess_data <- function(dataset){
#One Hot Encoding des jours de la semaine
jours <- unique(dataset$jour)
for(j in jours){
dataset[j] <- ifelse(dataset$jour==j, 1, 0)
}
#Création d'une colonne "intercept" a 1
dataset['intercept'] <- 1
#On conserve les caractéristiques qui nous intéresse
dataset <- dataset[,!names(dataset) %in% c('date', 'jour', 'dimanche')]
return(dataset)
}
Application
Nous sommes enfin prêts à lancer notre régression. Lors de la présentation du jeu de données, nous avions précisé que la période de 01/10/2016 au 15/10/2016 ne contenait aucune valeur d'audimat afin que nous puissions les prédire. Il va donc falloir penser à les supprimer temporairement le temps de l'apprentissage, par ailleurs il nous faut également isoler la variable cible (ici telespectateurs) dans un vecteur comme attendu par notre fonction.
#Preparation des donnees
dataf <- preprocess_data(df_audimat)
#Suppression des lignes dont la variable "telespectateurs" est a NA
dataf <- na.omit(dataf, cols=c('telespectateurs'))
#On isole la variable "telespectateurs" dans un dataframe target
target <- dataf[['telespectateurs']]
dataf <- subset(dataf, select=-c(telespectateurs))
#Enfin on lance la regression
resultats <- reg_lin(target, as.matrix(dataf))
Les coefficients estimés, retournés par la fonction, sont les suivants :
resultats[1]
temperature 0.16867565 precipitation -0.04061588 vendredi -3.07042530 samedi -2.37261347 lundi 3.50354390 mardi 4.37749652 mercredi 0.13102722 jeudi -2.10808103 intercept 45.72218296
Editons à présent les statistiques de tests t-value calculées par la fonction :
resultats[3]
temperature 11.0245058 precipitation -1.6823193 vendredi -7.4175706 samedi -5.7271465 lundi 8.4517642 mardi 10.5674279 mercredi 0.3160339 jeudi -5.0876756 intercept 124.5987897
Enfin, quelques statistiques concernant les résidus :
residus <- resultats[[4]]
print(paste0("Min : ", min(residus)))
print(paste0("Q1 : ", quantile(residus, probs = 0.25)))
print(paste0("Mediane : ", median(residus)))
print(paste0("Q3 : ", quantile(residus, probs = 0.75)))
print(paste0("Max : ", max(residus)))
Min : -17.9787651211641 Q1 : -3.71323146677442 Mediane : -0.170844904118994 Q3 : 3.58011451598181 Max : 26.1397106862696
Il convient de préciser qu'une étude des résidus peut s'avérer nécessaire pour valider les résultats des tests statistiques. Ainsi l'étude devra porter sur l'indépendance des résidus et leur distribution (normale et homogène).
Comparaison avec la fonction lm de R
Lançons à présent la fonction lm (linear model) de R afin de comparer nos résultats.
resultats_lm <- lm(telespectateurs ~ precipitation + temperature + jour, data=df_audimat)
summary(resultats_lm)
Residuals:
Min 1Q Median 3Q Max
-17.9788 -3.7132 -0.1708 3.5801 26.1397
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 45.72218 0.36696 124.599 < 2e-16 ***
precipitation -0.04062 0.02414 -1.682 0.0926 .
temperature 0.16868 0.01530 11.025 < 2e-16 ***
jourjeudi -2.10808 0.41435 -5.088 3.90e-07 ***
jourlundi 3.50354 0.41453 8.452 < 2e-16 ***
jourmardi 4.37750 0.41424 10.567 < 2e-16 ***
jourmercredi 0.13103 0.41460 0.316 0.7520
joursamedi -2.37261 0.41427 -5.727 1.15e-08 ***
jourvendredi -3.07043 0.41394 -7.418 1.63e-13 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.495 on 2454 degrees of freedom
(10 observations deleted due to missingness)
Multiple R-squared: 0.2275, Adjusted R-squared: 0.2249
F-statistic: 90.32 on 8 and 2454 DF, p-value: < 2.2e-16
Comme vous pouvez le constater, nos résultats sont identiques à ceux de la fonction native lm.
Prédictions
Le modèle étant implémenté, nous pouvons tenter de prédire l'audimat sur la période manquante. Nous repréparons notre jeu de données, cette fois sans supprimer les valeurs non définies de "telespectateurs"
data <- preprocess_data(df_audimat)
data <- subset(data, select=-c(telespectateurs))
Puis, nous effectuons nos prédictions sur l'ensemble de notre jeu de données grâce aux estimateurs calculés précédemment.
df_audimat['y_pred'] <- as.matrix(data)%*%resultats[[1]]
Visualisation
Afin de visualiser les valeurs d'audimat prédites nous allons les juxtaposer à celles des deux semaines précédentes sur un graphique. Pour cela nous extrayons dans deux dataframes distincts les périodes du 15 au 30 septembre puis partant du 01 octobre.
extract_obsv <- df_audimat[df_audimat$date >= as.Date("2016-09-15") & df_audimat$date < as.Date("2016-09-30"),]
extract_pred <- df_audimat[df_audimat$date >= as.Date("2016-10-01"),]
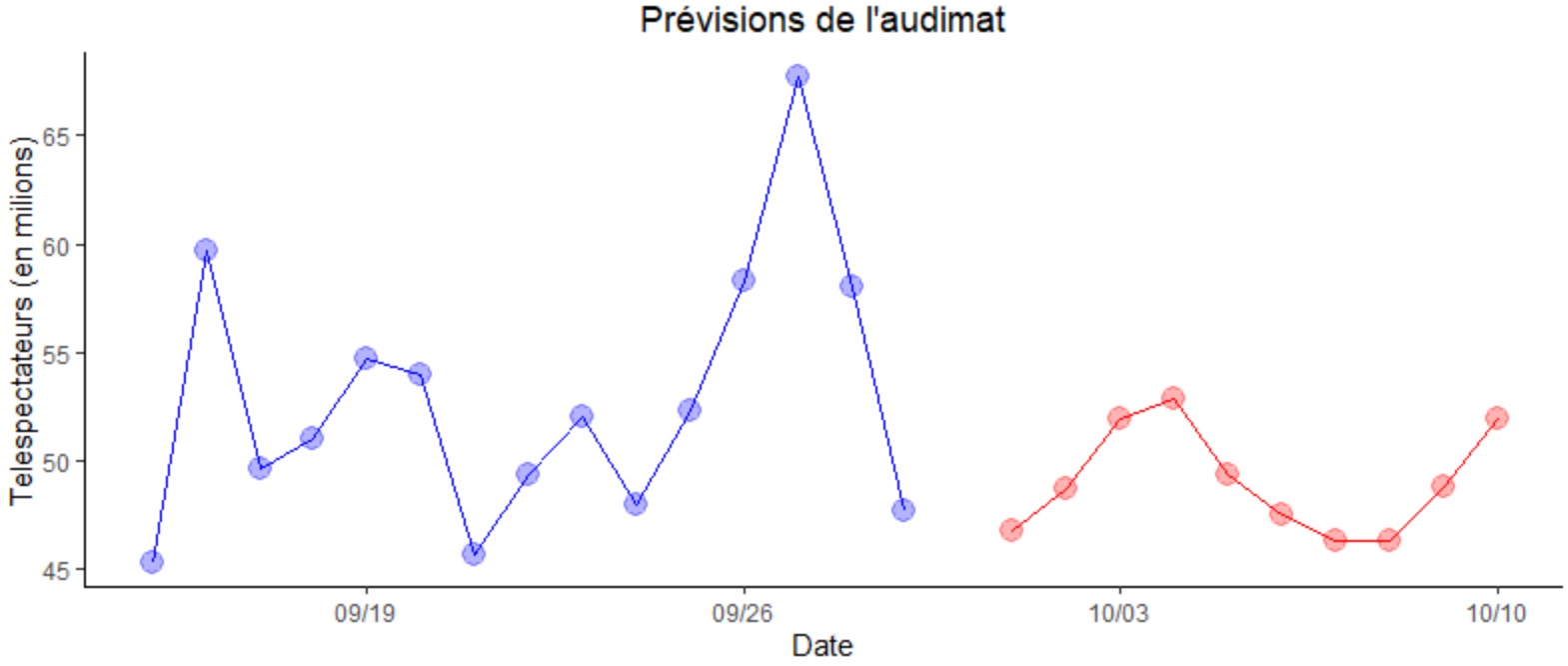
Il ne nous reste plus qu'à dresser le graphique correspondant. Ci-dessous, sur le graphique, en bleu les valeurs d'audimat observées fin septembre 2016 et en rouge les valeurs d'audimat prédites début octobre.
library(ggplot2)
theme_set(
theme_classic() +
theme(legend.position = "top")
)
p <- ggplot(data = extract_obsv, aes(x = date, y = telespectateurs))+
geom_line(color = "blue", size = 0.4)+
geom_point(color = "blue", size = 4, alpha=0.3)+
geom_line(data=extract_pred, aes(x=date, y=y_pred), color = "red", size = 0.4)+
geom_point(data=extract_pred, aes(x=date, y=y_pred), color = "red", size = 4, alpha=0.3)
p + scale_x_date(date_labels = "%m/%d")+
ggtitle("Prévisions de l'audimat")+
theme(plot.title = element_text(hjust = 0.5))+
labs(y="Telespectateurs (en milions)", x = "Date")
Retrouvez dans la rubrique "Nos datasets" toutes les données dont vous aurez besoin pour tester et pratiquer !

