Time series sous R et valeurs manquantes
Comment imputer les valeurs manquantes dans une série temporelle
Séries temporelles et valeurs manquantes ne font en général pas bon ménage. Si on se contente bien souvent
de les supprimer d'un échantillon lambda, le problème est diffèrent sur une série temporelle. La plupart des
modèles de prédiction travaille en effet sur des séries complètes, par ailleurs l'étude d'une éventuelle
saisonnalité peut s'en trouver fausser.
Nous allons voir les différentes techniques qu'il est possible de mettre en œuvre pour imputer, de façon
la plus transparente possible, les valeurs manquantes.
Données de travail
Pour illustrer nos propos, nous allons travailler avec, pour jeu de données, un échantillon listant les températures observées quotidiennement à Paris entre le 1er janvier 1999 et le 31 décembre 2009.
Chargeons nos données dans un dataframe "df_paris", et voyons à quoi elles ressemblent :
df_paris <- read.table("temperatures_paris.csv", header = TRUE,
sep = ",",
quote = "\"",
fill = TRUE,
comment.char = "",
encoding="UTF-8")
head(df_paris)
Month Day Year tcelcius 1 1 1 1999 8.4 2 1 2 1999 8.9 3 1 3 1999 9.6 4 1 4 1999 13.9 5 1 5 1999 12.3
Comme nous le voyons, la date d'observation fait l'objet de 3 variables distinctes : Month, Day et Year.
S'agissant d'une série temporelle, nous voulons travailler avec une variable date, nous allons donc créer une nouvelle
colonne : date_j
df_paris['date_j'] <- paste(sprintf("%02d", df_paris$Day),
sprintf("%02d", df_paris$Month),
df_paris$Year, sep='/')
df_paris[['date_j']] <- as.Date(df_paris[['date_j']], format='%d/%m/%Y')
head(df_paris)
Month Day Year tcelcius date_j 1 1 1 1999 8.4 1999-01-01 2 1 2 1999 8.9 1999-01-02 3 1 3 1999 9.6 1999-01-03 4 1 4 1999 13.9 1999-01-04 5 1 5 1999 12.3 1999-01-05
Détection des valeurs manquantes
Contrôlons à présent si certaines températures manquent à l'appel. S'agissant du sujet de cet article, il y a fort à parier qu'il y en ait ...
naValue <- df_paris[is.na(df_paris$tcelcius),]
cat("Nombre d'observations manquantes : ", nrow(naValue))
naValue
Nombre d'observations manquantes : 7
Month Day Year tcelcius date_j
1265 6 18 2002 NA 2002-06-18
1266 6 19 2002 NA 2002-06-19
1267 6 20 2002 NA 2002-06-20
1268 6 21 2002 NA 2002-06-21
2423 8 19 2005 NA 2005-08-19
3162 8 28 2007 NA 2007-08-28
3163 8 29 2007 NA 2007-08-29
Nous avons 7 valeurs manquantes qui prennent la valeur NA sous R. Nous avons pris soin de les stocker dans un dataframe dédié affiché ci-dessus. Nous remarquons qu'il y a 4 jours consécutifs en juin 2002, 1 journée isolée en aout 2005 et enfin 2 jours consécutifs en aout 2007.
Visualisation de la série
Visualisons à présent la série temporelle. Nous allons également en profiter pour faire figurer sur le graphique un repère (ligne pointillée rouge) à chaque valeur manquante.
library(ggplot2)
theme_set(theme_minimal())
p <- ggplot(data = df_paris, aes(x = date_j, y = tcelcius))+
geom_line(color = "#00AFBB", size = 0.6)
p + scale_x_date(date_labels = "%m/%Y")+
ggtitle("Valeurs de températures a Paris")+
theme(plot.title = element_text(hjust = 0.5))+
labs(y="Températures observées", x = "Jour") +
geom_vline(xintercept = naValue$date_j,
colour = 'red', linetype = "dashed")
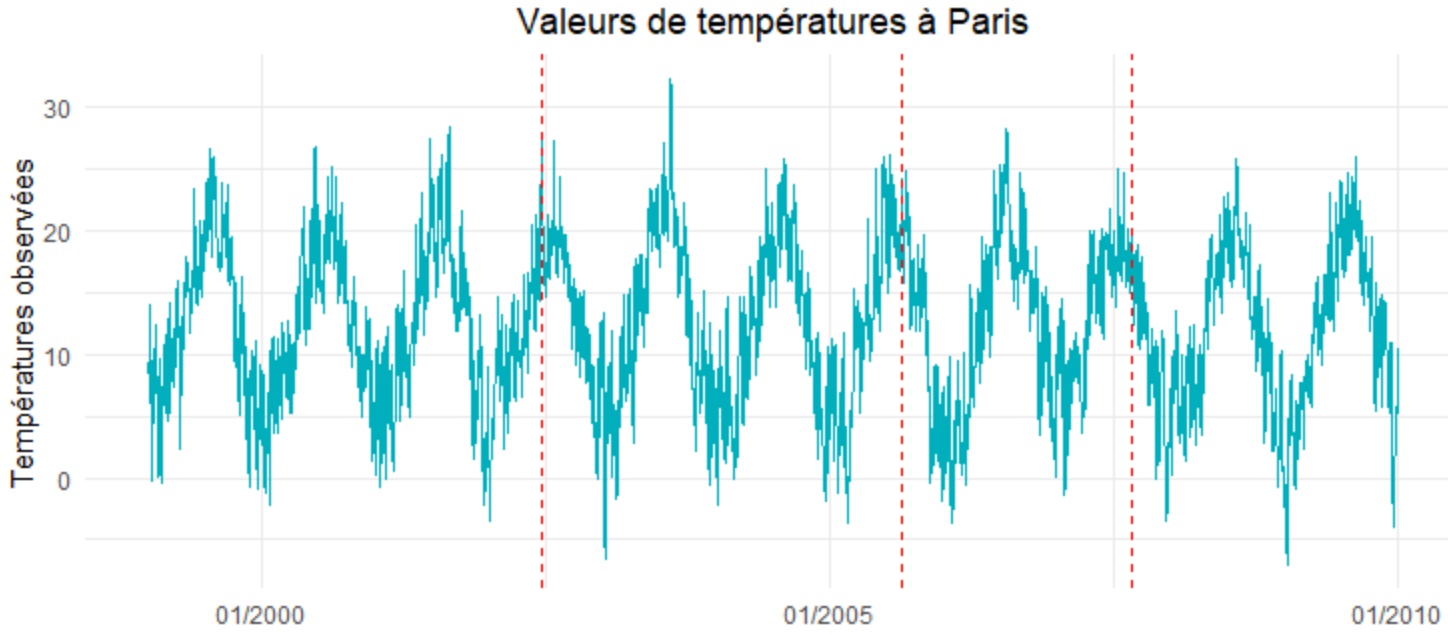
La présence d’une saisonnalité nous incite à agir de façon locale pour respecter, d’une part, la saison et, d’autre part,
le caractère exceptionnel que peut prendre la température sur une période donnée.
Le décor est posé, passons maintenant aux différentes techniques qui peuvent nous permettre de renseigner les valeurs
manquantes.
LOCF et NOCB
Derrière ces abréviations se cachent 2 premières techniques relativement simples. LOCF signifie Last Observation Carried
Forward et consiste à reconduire une valeur sur une date ultérieure. A l'inverse, NOCB signifie Next Observation
Carried backward et consiste, comme vous vous en doutez, à reconduire une valeur à une date anterieure.
Dans notre exemple, nous avions vu qu'il y avait 2 journées consécutives en aout 2007. Nous allons, pour illustrer les 2 méthodes
décrites ci-dessus, appliquer LOCF sur le 2007-08-28 et NOCB sur le 2007-08-29.
Listons tout d'abord une plage de valeurs fin aout 2007 avant intervention :
zoomDays <- seq(as.Date("2007-08-23"), as.Date("2007-08-30"), by="days")
df_paris[df_paris$date_j %in% zoomDays,]
Month Day Year tcelcius date_j
3157 8 23 2007 17.2 2007-08-23
3158 8 24 2007 18.4 2007-08-24
3159 8 25 2007 18.4 2007-08-25
3160 8 26 2007 19.6 2007-08-26
3161 8 27 2007 17.4 2007-08-27
3162 8 28 2007 NA 2007-08-28
3163 8 29 2007 NA 2007-08-29
3164 8 30 2007 15.4 2007-08-30
Imputons nos valeurs manquantes à présent, et listons de nouveau notre fenêtre :
valueLOCF <- df_paris[df_paris$date_j=='2007-08-27',4]
valueNOCB <- df_paris[df_paris$date_j=='2007-08-30',4]
df_paris[df_paris$date_j=='2007-08-28',4] <- valueLOCF
df_paris[df_paris$date_j=='2007-08-29',4] <- valueNOCB
df_paris[df_paris$date_j %in% zoomDays,]
Month Day Year tcelcius date_j
3157 8 23 2007 17.2 2007-08-23
3158 8 24 2007 18.4 2007-08-24
3159 8 25 2007 18.4 2007-08-25
3160 8 26 2007 19.6 2007-08-26
3161 8 27 2007 17.4 2007-08-27
3162 8 28 2007 17.4 2007-08-28
3163 8 29 2007 15.4 2007-08-29
3164 8 30 2007 15.4 2007-08-30
Nous pouvons constater que la valeur du 27 a été reconduite au 28, et la valeur du 30 a été reconduite au 29.
Moyenne et médiane
Une autre technique simple consiste à établir la moyenne des n valeurs situées avant et des n valeurs situées après. Il faudra
veiller à ne pas prendre une fenêtre n trop importante si les données sont sujettes à des pics de forte amplitude.
Nous allons illustrer cette technique sur la valeur manquante du 19 aout 2005. Nous allons établir pour cela une moyenne des
valeurs des températures observées du 17 au 21, soit 2 jours avant et 2 jours après.
Listons tout d'abord une fenêtre avant intervention :
zoomDays <- seq(as.Date("2005-08-16"), as.Date("2005-08-22"), by="days")
df_paris[df_paris$date_j %in% zoomDays,]
Month Day Year tcelcius date_j
2420 8 16 2005 18.2 2005-08-16
2421 8 17 2005 21.6 2005-08-17
2422 8 18 2005 24.2 2005-08-18
2423 8 19 2005 NA 2005-08-19
2424 8 20 2005 16.9 2005-08-20
2425 8 21 2005 17.1 2005-08-21
2426 8 22 2005 18.4 2005-08-22
Puis la même chose après avoir calculé la moyenne :
nearestDays <- seq(as.Date("2005-08-17"), as.Date("2005-08-21"), by="days")
valeurMoyenne <- mean(df_paris[df_paris$date_j %in% nearestDays, 4], na.rm = TRUE)
df_paris[df_paris$date_j=='2005-08-19',4] <- valeurMoyenne
df_paris[df_paris$date_j %in% zoomDays,]
Month Day Year tcelcius date_j
2420 8 16 2005 18.20 2005-08-16
2421 8 17 2005 21.60 2005-08-17
2422 8 18 2005 24.20 2005-08-18
2423 8 19 2005 19.95 2005-08-19
2424 8 20 2005 16.90 2005-08-20
2425 8 21 2005 17.10 2005-08-21
2426 8 22 2005 18.40 2005-08-22
Nous ne reconduisons pas cet exemple avec la médiane car le code est identique à l'exception de la fonction mean à remplacer par median.
Interpolation linéaire
Les techniques précédentes peuvent s'appliquer lorsque les plages sont réduites. Les appliquer sur un trop grand nombre de jours
consécutifs induirait la création d'escaliers ou de plateaux artificiels. Même si l'interpolation linéaire ne saurait remplacer
l'exactitude des données originales, elle constitue un moindre mal et offre une meilleure alternative. Son principe est simple puisque
l'interpolation linéaire va tracer une droite entre 2 valeurs connues pour y aligner les valeurs manquantes.
Comme pour nos exemples précédents, affichons une fenêtre incluant les jours à traiter :
zoomDays <- seq(as.Date("2002-06-16"), as.Date("2002-06-23"), by="days")
df_paris[df_paris$date_j %in% zoomDays,]
Month Day Year tcelcius date_j
1263 6 16 2002 23.1 2002-06-16
1264 6 17 2002 27.7 2002-06-17
1265 6 18 2002 NA 2002-06-18
1266 6 19 2002 NA 2002-06-19
1267 6 20 2002 NA 2002-06-20
1268 6 21 2002 NA 2002-06-21
1269 6 22 2002 22.2 2002-06-22
1270 6 23 2002 18.7 2002-06-23
Nous allons maintenant calculer les 4 valeurs manquantes ci-dessus avec la fonction native approx. Il existe également
une fonction bien connue na.approx dans la librairie zoo qui fait la même chose.
Il restera ensuite à réintroduire ces valeurs interpolées dans le dataframe d'origine df_paris, mais notez que nous aurions
pu soumettre directement tout le dataframe a l'interpolation.
interpoledValues <- df_paris[df_paris$date_j %in% zoomDays,]
interpoledValues <- data.frame(approx(interpoledValues$date_j,
interpoledValues$tcelcius,
xout = interpoledValues$date_j,
rule = 2,
method = "linear",
ties = mean))
interpoledValues
x y
1 2002-06-16 23.1
2 2002-06-17 27.7
3 2002-06-18 26.6
4 2002-06-19 25.5
5 2002-06-20 24.4
6 2002-06-21 23.3
7 2002-06-22 22.2
8 2002-06-23 18.7
Retrouvez dans la rubrique "Nos datasets" toutes les données dont vous aurez besoin pour tester et pratiquer !

