Test de normalité sous R

Validez l'hypothèse de normalité d'une distribution avant l'emploi de tests statistiques

Nombre de tests statistiques, Pearson par exemple, pour ne citer que celui-ci, partent de l'hypothèse que les valeurs d'une variable sont distribuées normalement. La rigueur voudrait donc que cette hypothèse soit validée préalablement au test. Il existe plusieurs façons de valider la normalité, voyons comment procéder :

Données de travail

Pour illustrer nos propos, nous allons travailler avec, pour jeu de données, un échantillon listant les âges des enfants et adolescents qui fréquentent un skate-park. Nous avons un effectif de 160 individus pour une seule variable observée : l’âge.

Chargeons nos données dans un "df_skate" :

df_skate <- read.table("skate_park.csv", header = TRUE,
                       sep = ";",
                       quote = "\"",
                       fill = TRUE,
                       comment.char = "",
                       encoding="UTF-8")

Approche empirique

Constater ou non la normalité d'une variable peut s'effectuer via une première approche empirique en dressant puis analysant des graphiques. Quels graphiques peuvent nous permettre de statuer sur l'hypothèse de normalité ?
Nous allons en produire deux : l'histogramme et le box-plot.

library(ggplot2)
theme_set(
  theme_classic() + 
    theme(legend.position = "top")
)

color <- "#00AFBB"

# Histogramme
ggplot(df_skate, aes(x = age, y=..count..)) +
  geom_histogram(color = color, fill = color, 
                 bins = 16, alpha = 0.4) +
  ggtitle("Membres du Skate Park") +
  xlab("Age") + ylab("Effectif") +
  theme(
    plot.title = element_text(size=9, hjust = 0.5, face="bold", color="black"),
    axis.title = element_text(size=9)
  )

# Boxplot
ggplot(df_skate, aes(x=factor(0), y=age)) + 
  geom_boxplot(fill=color, alpha=0.4) +
  ggtitle("Boxplot") +
  ylab("Age") +
  theme(
    plot.title = element_text(size=9, hjust = 0.5, face="bold", color="black"),
    axis.title = element_text(size=9),
    axis.title.x=element_blank(),
    axis.text.x=element_blank(),
    axis.ticks.x=element_blank()) 

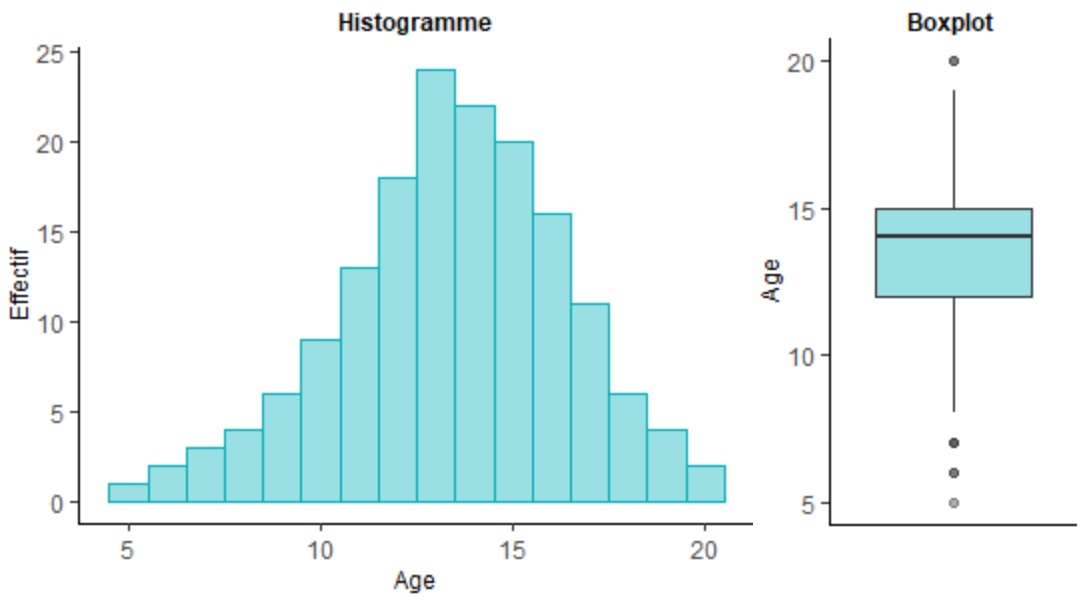
Si l’âge est distribué normalement, nous nous attendons à trouver un histogramme en forme de cloche, or bien que nous constations une forme qui s'en approche, nous percevons néanmoins une légère asymétrie qui tend vers les âges plus élevés. Il semble en effet que l'essentiel des effectifs se situe dans une fourchette 12 ~ 16 ans. Le bloxplot, qui se base de son coté sur la dispersion autour de la médiane, nous conforte dans notre première analyse. Bien que les pattes soient proportionnées et de longueur équivalente, le box-plot n'est pas équilibré, la médiane se situe en effet plutôt vers le haut de la boite.
Cette première analyse devrait suffire à conclure que l'hypothèse de normalité est rejetée sur cet échantillon.

Diagramme quantile-quantile

Le diagramme quantile-quantile ou qqplot va nous permettre de comparer la position de certains quantiles entre notre échantillon et une population dite théorique distribuée selon une loi classique. En l'occurrence nous voulons une comparaison avec une distribution selon la loi normale.
Traçons le qqplot :

qplot(data= df_skate, sample = age) + 
  stat_qq(colour = "#00AFBB") + 
  stat_qq_line(distribution = qnorm, col = "red") +
  scale_color_manual(values = "#00AFBB")+
  ggtitle("Diagramme quantile-quantile") +
  ylab("Age") +
  theme(
    plot.title = element_text(size=9, hjust = 0.5, face="bold", color="black"),
    axis.title = element_text(size=9)
  )

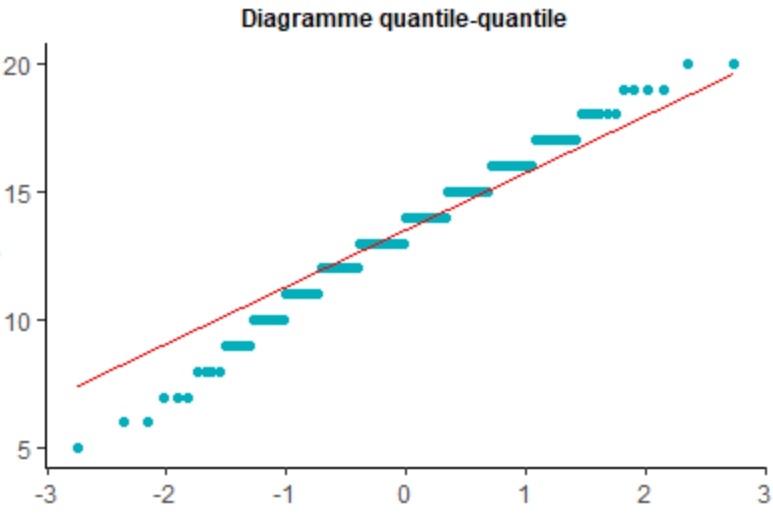
Nous avons dans le code ci-dessus précisé dans la fonction qq_line que nous voulions une distribution théorique normale, or il s'agit de la loi par défaut donc nous aurions pu nous en passer. Il faut savoir néanmoins que le qqplot peut servir pour d'autres lois ...
Nous voyons que la distribution de notre variable âge ondule autour de la droite normale théorique sans jamais s'aligner vraiment avec. Ceci est particulièrement vrai autour des plus jeunes qui sont, a priori, en sous-effectifs.

Asymétrie et aplatissement de Fisher

Les coefficients d’asymétrie (skewness) et d’aplatissement (kurtosis) de Fisher sont des indicateurs de la forme d'une distribution. Une distribution normale aura des coefficients d'asymétrie comme d'aplatissement nuls.
Calculons ces coefficients pour notre échantillon.

library(e1071)
skewness(df_skate$age)
kurtosis(df_skate$age)

> skewness(df_skate$age)
[1] -0.2966519
> kurtosis(df_skate$age)
[1] -0.04649954

Le coefficient d'aplatissement (kurtosis) est plutôt proche de 0, par contre le coefficient d'asymétrie (skewness) est bien inférieur a 0. Cela marque un étalement vers la gauche et donc une asymétrie marquée à droite, vers les âges élevés.

Test statistique de Shapiro-Wilk

Le test de Shapiro-Wilk part de l'hypothèse nulle selon laquelle l'échantillon est normalement distribué. Par conséquent si la p-value retournée par ce test est inférieure au seuil alpha de 5% nous rejetterons l'hypothèse nulle et pourrons considérer que notre variable âge ne suit pas une loi normale.
Voyons ceci :

shapiro.test(df_skate$age)

Shapiro-Wilk normality test

data:  df_skate$age
W = 0.98273, p-value = 0.0421

Nous constatons en effet que la p-value est située sous le seuil des 5%. Notre hypothèse de normalité est donc rejetée. Ceci vient confirmer tout ce que les graphiques nous ont dit auparavant.

Retrouvez dans la rubrique "Nos datasets" toutes les données dont vous aurez besoin pour tester et pratiquer !