Lissage par moyenne mobile sous R
Lisser une série temporelle sur la base d'une moyenne mobile simple ou centrée
Nous avons évoqué dans un précèdent article l'imputation des valeurs manquantes dans une série temporelle. Nous allons ici continuer sur les séries temporelles et voir comment procéder a un lissage sur la base des moyennes mobiles.
Données de travail
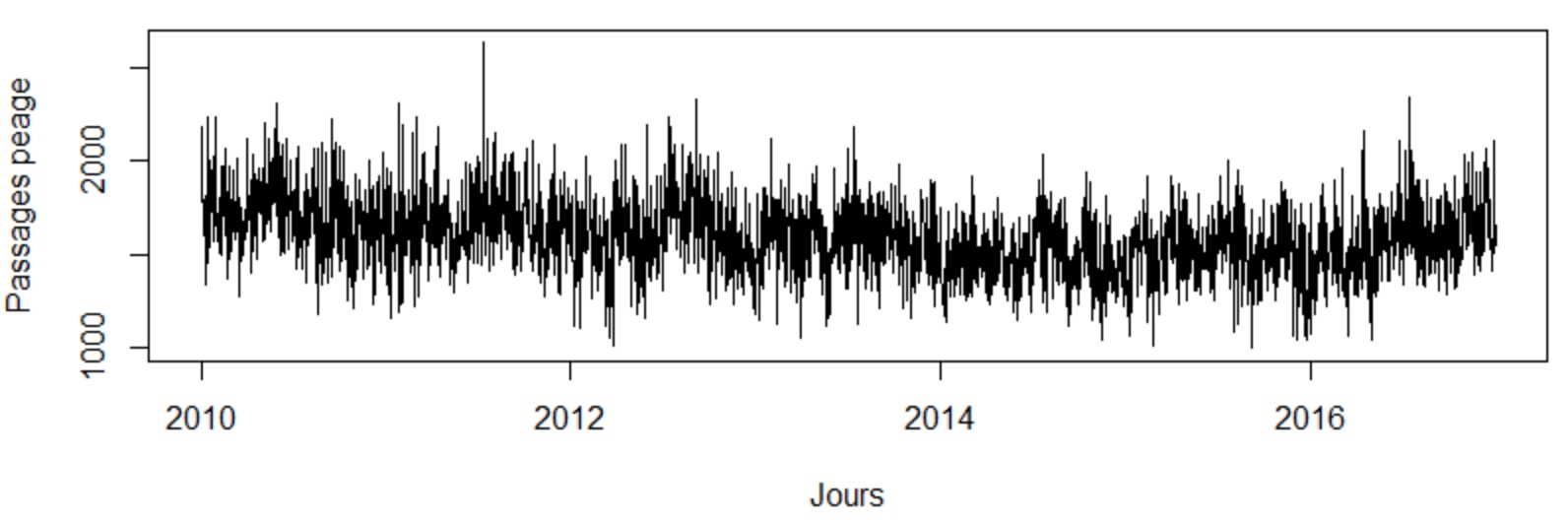
La série sur laquelle nous allons nous baser retrace la fréquentation, en nombre de véhicules, d'un péage d'autoroute. Cette série couvre une période journalière allant du 01 janvier 2010 au 26 octobre 2016.
Chargeons nos données dans un dataframe "df_peage", et voyons à quoi elles ressemblent :
df_peage <- read.table("peage.csv", header = TRUE,
sep = ",",
quote = "\"",
fill = TRUE,
comment.char = "",
encoding="UTF-8")
head(df_peage)
jour mois annee passages 1 1 1 2010 1782 2 2 1 2010 2178 3 3 1 2010 1804 4 4 1 2010 1892 5 5 1 2010 1716 6 6 1 2010 1771
Nous constatons que la date d'observation fait l'objet de 3 variables distinctes : année, mois et jour.
A l'instar de ce que nous avions fait dans notre précèdent article sur les séries temporelles,
nous allons créer une nouvelle colonne : date_jour de format Date.
df_peage['date_jour'] <- paste(sprintf("%02d", df_peage$jour),
sprintf("%02d", df_peage$mois),
df_peage$annee, sep='/')
df_peage[['date_jour']] <- as.Date(df_peage[['date_jour']], format='%d/%m/%Y')
head(df_peage)
jour mois annee passages date_jour 1 1 1 2010 1782 2010-01-01 2 2 1 2010 2178 2010-01-02 3 3 1 2010 1804 2010-01-03 4 4 1 2010 1892 2010-01-04 5 5 1 2010 1716 2010-01-05 6 6 1 2010 1771 2010-01-06
Visualisations nos données :
Moyenne mobile simple et moyenne mobile centrée
Lisser les données au moyen d'une moyenne mobile d'ordre p va consister à définir une fenêtre
de p périodes afin d'effectuer la moyenne des valeurs couvertes. Cette moyenne sera ensuite
affectée à la période centrale. La fenêtre va ainsi se déplacer du début à la fin de la
série a lisser.
On comprend aisément qu'un ordre impair ne pose pas de problème quand à la détermination
de la période qui va porter la moyenne, ceci est moins évident dans le cas d'un ordre pair. C'est
ici qu'intervient la notion de moyenne centrée, puisqu'elle va consister, dans le cas d'un ordre pair,
à établir, d'une part, une fenêtre de p+1 périodes et, d'autre part, à pondérer la première et la dernière
période par 1/2.
Voyons tout ceci en détails.
Moyenne mobile simple
Ci-dessous une fonction lissage qui va prendre en paramètres d'entrée la série
numérique a lisser (var_num), la taille de la fenêtre (alpha) ainsi que la série temporelle
(var_temps).
Apres avoir calculé la demie fenêtre (division entière de la fenêtre alpha), la fonction lissage
va parcourir la série numérique afin d'effectuer la moyenne des valeurs couvertes. Il s'agit donc
d'une moyenne mobile simple.
lissage <- function(var_num, alpha, var_temps){
n = length(var_num)
#Initialisation des vecteurs de sortie
valeurs_lissees <- c()
vecteur_temps <- c()
#Nous parcourons la série en prenant soin de soustraire alpha à la borne sup.
demieFenetre <- alpha%/%2
for (i in demieFenetre:(n-demieFenetre)){
valeurs_lissees <- c(valeurs_lissees,
(sum(var_num[(i-demieFenetre):(i+demieFenetre)],
na.rm = TRUE)/alpha))
vecteur_temps <- c(as.Date(vecteur_temps), var_temps[i])
}
return(list(valeurs_lissees, vecteur_temps))
}
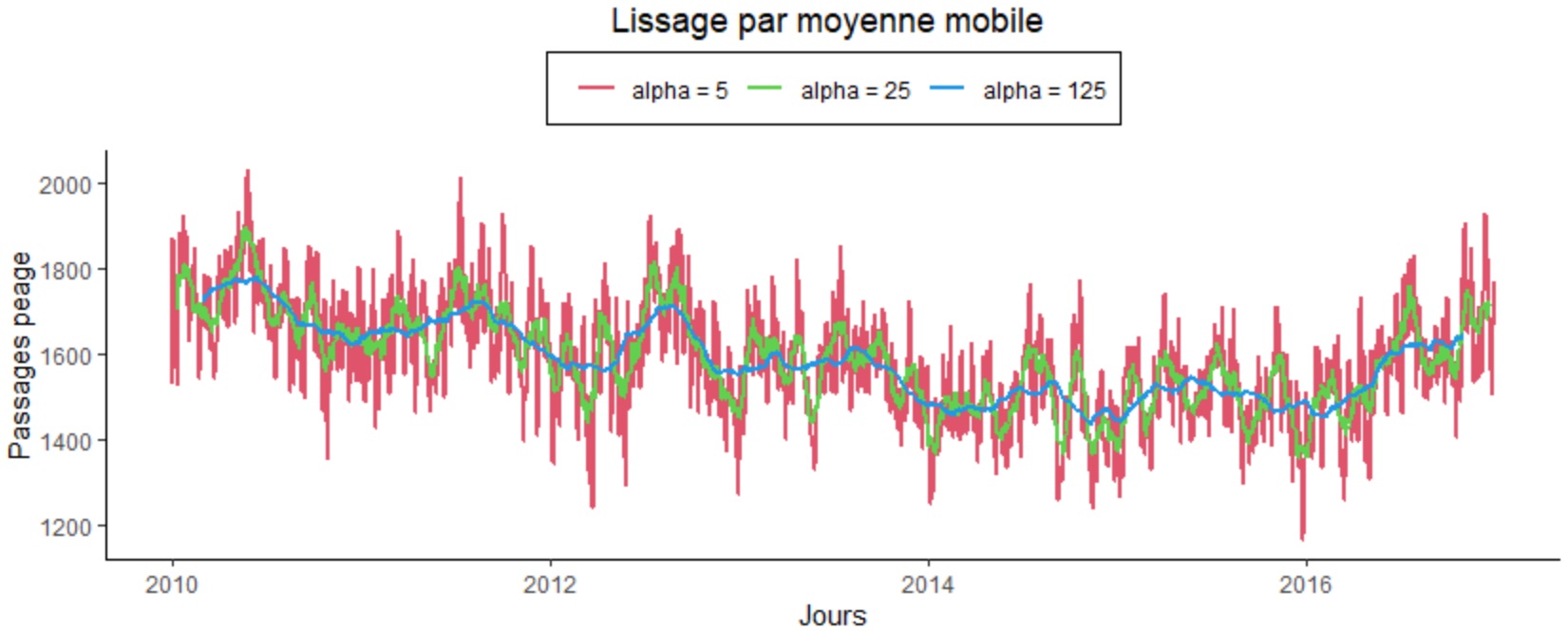
Voyons le résultat obtenu pour des ordres de 5 jours, 25 jours et 155 jours.
Pour cela nous définissons notre collection d'ordres alpha et de couleurs associées.
alpha_collection <- c(5, 55, 125)
alpha_couleurs <- c(2, 3, 4)
Nous lançons ensuite la fonction lissage pour chacun des ordres à éditer. Les données propres aux moyennes mobiles seront stockées dans un dataframe mvDf.
mvDf <- data.frame()
for (alpha in alpha_collection){
mvData <- lissage(df_peage$passages, alpha, df_peage$date_jour)
mvData <- as.data.frame(mvData, col.names = c('mav', 'date_jour'))
mvData['alpha'] = alpha
mvData['couleur'] = alpha_couleurs[which(alpha == alpha_collection)]
mvDf <- rbind(mvDf, mvData)
}
Enfin il ne nous reste plus qu'a dresser le graphique.
library(ggplot2)
theme_set(
theme_classic() +
theme(legend.position = "top")
)
p <- ggplot(data = mvDf, aes(x = date_jour, y = mav))+
geom_line(aes(group = couleur, color = as.factor(couleur)), size = 1)
p + ggtitle("Lissage par moyenne mobile ")+
theme(plot.title = element_text(hjust = 0.5),
legend.title=element_blank(),
legend.background = element_rect(linetype = 1, size = 0.5, colour = 1))+
labs(y="Entrées", x = "Jours")+
scale_color_manual(labels = paste0("alpha = ", alpha_collection),
values = alpha_couleurs)
Moyenne mobile centrée
La fonction lissage illustrée précédemment peut être plus précise sur les lissages d'ordre pair, aussi nous allons la modifier pour les prendre en compte.
lissage <- function(var_num, alpha, var_temps){
n = length(var_num)
#Initialisation des vecteurs de sortie
valeurs_lissees <- c()
vecteur_temps <- c()
#Nous parcourons la série en prenant soin de soustraire alpha à la borne sup.
demieFenetre <- alpha%/%2
for (i in demieFenetre:(n-demieFenetre)){
#Lissage centre
if(alpha%%2==0){
valeurs_lissees <- c(valeurs_lissees,
(sum(var_num[(i-demieFenetre)]/2,
var_num[(i-demieFenetre+1):(i+demieFenetre-1)],
var_num[(i+demieFenetre)]/2,
na.rm = TRUE)/alpha))
#Lissage simple
}else{
valeurs_lissees <- c(valeurs_lissees,
(sum(var_num[(i-demieFenetre):(i+demieFenetre)],
na.rm = TRUE)/alpha))
}
vecteur_temps <- c(as.Date(vecteur_temps), var_temps[i])
}
return(list(valeurs_lissees, vecteur_temps))
}
La seule différence notable réside dans le test sur la parité de l'ordre alpha. Pour un alpha pair, la calcul de la moyenne est diffèrent dans la mesure ou on attribue un poids de 1/2 au premier et dernier terme de la somme.
Retrouvez dans la rubrique "Nos datasets" toutes les données dont vous aurez besoin pour tester et pratiquer !

